Transform 22
Tutorials

SplitBregman: enforce sparsity

Authors
Affiliations

The Split-Bregman Algorithm: Sparsity Enforcing Inversions

@Author: Francesco Picetti - picettifrancesco@gmail.com

In this notebook we will show the Split-Bregman algorithm, as described by Goldstein and Osher, 2009.

In its generalized unconstrained formulation (the same we handle in this library), this algorithm takes what we call GeneralizedLasso (see occamypy.problem module):

arg⁡min⁡x∥Ax−d∥22+ε∥RL1x∥1,\begin{equation} \arg \min_\mathbf{x} \Vert \mathbf{A} \mathbf{x} - \mathbf{d}\Vert_2^2 + \varepsilon \Vert \mathbf{R}_{L1} \mathbf{x}\Vert_1, \end{equation}
(1)

being x\mathbf{x} our model, d\mathbf{d} the observed data, A\mathbf{A} a linear modeling operator, RL1\mathbf{R}_{L1} the sparsity promoting regularizer and its weight ε\varepsilon.

Import modules

# Importing necessary modules
import numpy as np
import occamypy as o

# Plotting
from matplotlib import rcParams
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib.pyplot as plt
rcParams.update({
    'image.cmap'     : 'gray',
    'image.aspect'   : 'auto',
    'image.interpolation': None,
    'axes.grid'      : True,
    'figure.figsize' : (12, 3),
    'savefig.dpi'    : 300,
    'axes.labelsize' : 14,
    'axes.titlesize' : 16,
    'font.size'      : 14,
    'legend.fontsize': 14,
    'xtick.labelsize': 14,
    'ytick.labelsize': 14,
    'text.usetex'    : True,
    'font.family'    : 'serif',
    'font.serif'     : 'Latin Modern Roman',
})
WARNING! DATAPATH not found. The folder /tmp will be used to write binary files

/Users/francesco/miniconda3/envs/swung/lib/python3.10/site-packages/dask_jobqueue/core.py:20: FutureWarning: tmpfile is deprecated and will be removed in a future release. Please use dask.utils.tmpfile instead.
  from distributed.utils import tmpfile

Example 1: 1D Ricker Deconvolution

In this example we want to invert a 1D seismic trace for the Earth's reflectivity. We suppose the wavelet to be known, yielding to a deterministic deconvolution problem.

# load wavelet
wav = o.VectorNumpy(np.load("./data/ricker20.npy"), ax_info=[o.AxInfo(n=51, o=0., d=0.002, l="time [s]")])

# load reflectivity
x = o.VectorNumpy(np.load("./data/reflectivity1D.npy"), ax_info=[o.AxInfo(n=1000, o=0., d=0.002, l="time [s]")])

# instantating operator
W = o.ConvND(x, wav)

# Generating true recorded trace
d = W * x

# Compute spectra
nfft = 4096
x_spectra = np.fft.fft(x.getNdArray(), nfft)
d_spectra = np.fft.fft(d.getNdArray(), nfft)
w_spectra = np.fft.fft(wav.getNdArray(), nfft)
freq = np.fft.fftfreq(nfft, wav.ax_info[0].d)
time_axis = x.ax_info[0].plot()
xlim = x.ax_info[0].o, x.ax_info[0].last
xlbl = x.ax_info[0].l
fig, ax = plt.subplots()
plt.plot(freq[:nfft//4], np.abs(x_spectra)[:nfft//4], 'k',  label='model')
plt.plot(freq[:nfft//4], np.abs(d_spectra)[:nfft//4], 'b',  label='data')
plt.legend(loc='upper right')
plt.xlabel("Frequency [Hz]"), plt.ylabel("Amplitude")
plt.xlim(0,100), plt.ylim(0,30)
plt.tight_layout(pad=0.5)
plt.show()

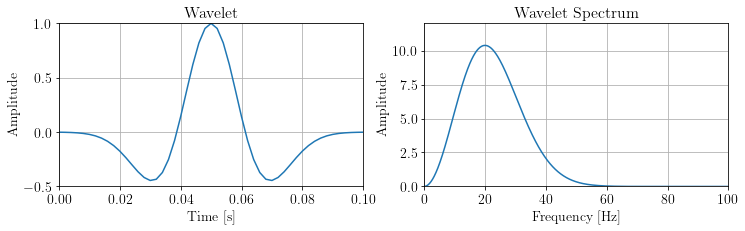
fig, ax = plt.subplots(1,2)
ax[0].plot(wav.ax_info[0].plot(), wav.plot())
ax[0].set_title('Wavelet')
ax[0].set_xlabel("Time [s]"), ax[0].set_ylabel("Amplitude")
ax[0].set_xlim(0,0.1), ax[0].set_ylim(-0.5,1)

ax[1].plot(freq[:nfft//4], np.abs(w_spectra)[:nfft//4])
ax[1].set_title('Wavelet Spectrum')
ax[1].set_xlabel("Frequency [Hz]"), ax[1].set_ylabel("Amplitude")
ax[1].set_xlim(0,100), ax[1].set_ylim(0,12)
plt.show()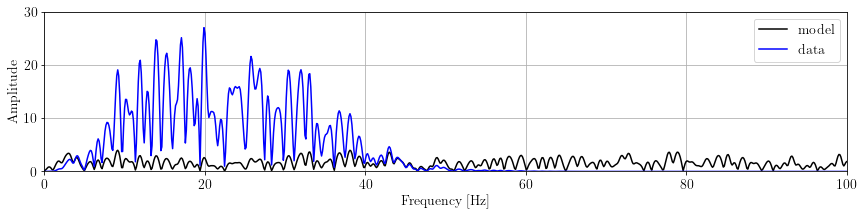
<Figure size 864x216 with 1 Axes><Figure size 864x216 with 2 Axes>
fig, ax = plt.subplots()
ax.plot(time_axis, x.plot(), 'k',  label='model')
ax.plot(time_axis, d.plot(), 'b',  label='data')
ax.legend(loc='upper left')
ax.set_ylim(-1., 1.), ax.set_xlim(*xlim)
ax.set_xlabel(xlbl), ax.set_ylabel("Amplitude")

axins1 = ax.inset_axes([0.42, 0.55, 0.1, 0.4])
axins1.plot(time_axis, x.plot(), 'k')
axins1.plot(time_axis, d.plot(), 'b')
axins1.set_xlim(0.76, 0.8)
axins1.set_ylim(-.1, .1)
axins1.set_xticklabels('')
axins1.set_yticklabels('') 
ax.indicate_inset_zoom(axins1)

axins2 = ax.inset_axes([0.55, 0.55, 0.1, 0.4])
axins2.plot(time_axis, x.plot(), 'k')
axins2.plot(time_axis, d.plot(), 'b')
axins2.set_xlim(1.51, 1.59)
axins2.set_ylim(-.1, .1)
axins2.set_xticklabels('')
axins2.set_yticklabels('') 
ax.indicate_inset_zoom(axins2)

axins3 = ax.inset_axes([0.49, 0.05, 0.1, 0.4])
axins3.plot(time_axis, x.plot(), 'k')
axins3.plot(time_axis, d.plot(), 'b')
axins3.set_xlim(1.0, 1.2)
axins3.set_ylim(-.1, .1)
axins3.set_xticklabels('')
axins3.set_yticklabels('') 
ax.indicate_inset_zoom(axins3)

plt.suptitle("Model and Data")
plt.show()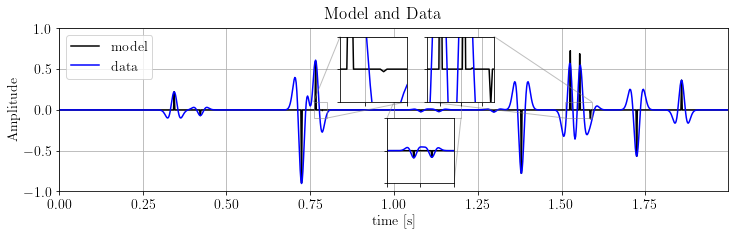
<Figure size 864x216 with 1 Axes>

Solve with Conjugate Gradient

Conjugate gradient is a fast and powerful adjoint-state algorithm for solving problems in the form:

x^=arg⁡min⁡x∥Wx−d∥22\begin{equation} \hat{\mathbf{x}} = \arg \min_\mathbf{x} \Vert \mathbf{W}\mathbf{x} - \mathbf{d}\Vert_2^2 \end{equation}
(2)
# instantiate a linear L2 problem
problemCG = o.LeastSquares(x.clone().zero(), d, W)

# define the solver with 10'000 iterations
CG = o.CG(o.BasicStopper(10000))
CG.setDefaults(save_obj=True)

# solve the problem
CG.run(problemCG, verbose=False)
fig, ax = plt.subplots()
ax.plot(time_axis, x.plot(), 'b', lw=2, label='true model')
ax.plot(time_axis, problemCG.model.plot(), 'r',  label='CG')
ax.legend(loc='upper left')
ax.set_ylim(-1., 1.), ax.set_xlim(*xlim)
ax.set_xlabel(xlbl), ax.set_ylabel("Amplitude")

axins1 = ax.inset_axes([0.42, 0.55, 0.1, 0.4])
axins1.plot(time_axis, x.plot(), 'b', lw=2)
axins1.plot(time_axis, problemCG.model.plot(), 'r')
axins1.set_xlim(0.76, 0.8)
axins1.set_ylim(-.1, .1)
axins1.set_xticklabels('')
axins1.set_yticklabels('') 
ax.indicate_inset_zoom(axins1)

axins2 = ax.inset_axes([0.55, 0.55, 0.1, 0.4])
axins2.plot(time_axis, x.plot(), 'b', lw=2)
axins2.plot(time_axis, problemCG.model.plot(), 'r')
axins2.set_xlim(1.51, 1.59)
axins2.set_ylim(-.1, .1)
axins2.set_xticklabels('')
axins2.set_yticklabels('') 
ax.indicate_inset_zoom(axins2)

axins3 = ax.inset_axes([0.49, 0.05, 0.1, 0.4])
axins3.plot(time_axis, x.plot(), 'b', lw=2)
axins3.plot(time_axis, problemCG.model.plot(), 'r')
axins3.set_xlim(1.0, 1.2)
axins3.set_ylim(-.1, .1)
axins3.set_xticklabels('')
axins3.set_yticklabels('') 
ax.indicate_inset_zoom(axins3)

plt.suptitle('Conjugate Gradient, %d it' % len(CG.obj))
plt.show()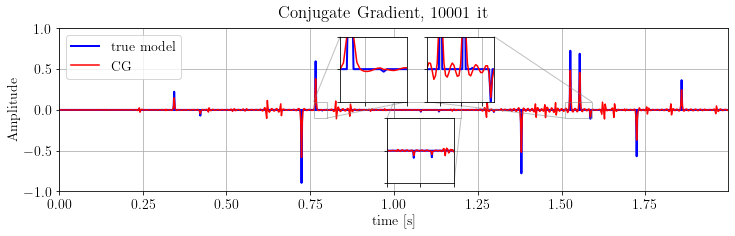
<Figure size 864x216 with 1 Axes>

Impose sparsity in the solution: FISTA

Iterative Shrinkage-Thresholding Algorithms solve the so-called LASSO problem:

x^=arg⁡min⁡x∥Wx−d∥22+λ∥x∥1\begin{equation} \hat{\mathbf{x}} = \arg \min_\mathbf{x} \Vert \mathbf{W}\mathbf{x} - \mathbf{d}\Vert_2^2 + \lambda \Vert \mathbf{x}\Vert_1 \end{equation}
(3)

If we provide the operator's maximum eigenvalue η\eta we can build a fast version of this algorithm by imposing the step α<1/η2\alpha < 1/\eta^2 as proposed in Beck and Teboulle, 2009.

compute maximum eigenvalue

maxeig = W.powerMethod()
print('FISTA α=%.6e' % (1/(maxeig**2)))
FISTA α=9.288532e-03

# define the LASSO problem
problemFISTA = o.Lasso(x.clone().zero(), d, W, lambda_value=1, op_norm=maxeig**2)

# instantiate the fast solver with 1000 iterations
FISTA = o.ISTA(o.BasicStopper(10000), fast=True)
FISTA.setDefaults(save_obj=True)

# solve the problem
FISTA.run(problemFISTA, verbose=False)
fig, ax = plt.subplots()
ax.plot(time_axis, x.plot(), 'b', lw=2, label='true model')
ax.plot(time_axis, problemFISTA.model.plot(), 'r',  label='FISTA')
ax.legend(loc='upper left')
ax.set_ylim(-1., 1.), ax.set_xlim(*xlim)
ax.set_xlabel(xlbl), ax.set_ylabel("Amplitude")

axins1 = ax.inset_axes([0.42, 0.55, 0.1, 0.4])
axins1.plot(time_axis, x.plot(), 'b', lw=2)
axins1.plot(time_axis, problemFISTA.model.plot(), 'r')
axins1.set_xlim(0.76, 0.8)
axins1.set_ylim(-.1, .1)
axins1.set_xticklabels('')
axins1.set_yticklabels('') 
ax.indicate_inset_zoom(axins1)

axins2 = ax.inset_axes([0.55, 0.55, 0.1, 0.4])
axins2.plot(time_axis, x.plot(), 'b', lw=2)
axins2.plot(time_axis, problemFISTA.model.plot(), 'r')
axins2.set_xlim(1.51, 1.59)
axins2.set_ylim(-.1, .1)
axins2.set_xticklabels('')
axins2.set_yticklabels('') 
ax.indicate_inset_zoom(axins2)

axins3 = ax.inset_axes([0.49, 0.05, 0.1, 0.4])
axins3.plot(time_axis, x.plot(), 'b', lw=2)
axins3.plot(time_axis, problemFISTA.model.plot(), 'r')
axins3.set_xlim(1.0, 1.2)
axins3.set_ylim(-.1, .1)
axins3.set_xticklabels('')
axins3.set_yticklabels('') 
ax.indicate_inset_zoom(axins3)

plt.suptitle(r'Fast-ISTA, $\lambda=$%.e, %d it' % (problemFISTA.lambda_value, len(FISTA.obj)))
plt.show()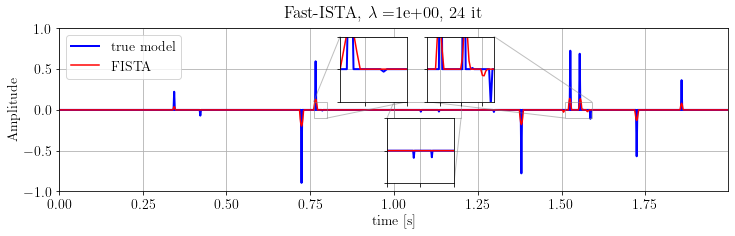
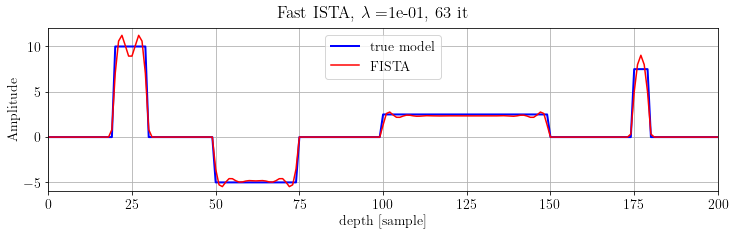
<Figure size 864x216 with 1 Axes>

Note that FISTA is able to recover the model's kinematics but not the true amplitude. Indeed, this algorithm is very sensitive to λ\lambda parameter. Let's try another solver.

Split-Bregman for LASSO problem

# define the Linear Regularized Problem
problemSB = o.GeneralizedLasso(x.clone().zero(), d, W, reg=o.Identity(x), eps=.1)

# instantiate the Split-Bregman solver
SB = o.SplitBregman(o.BasicStopper(1000), niter_inner=3, niter_solver=5,
                    linear_solver='LSQR', breg_weight=1., warm_start=True)
SB.setDefaults(save_obj=True)
# solve the problem
SB.run(problemSB, verbose=False, inner_verbose=False)
its = "%d-%d-%d" % (len(SB.obj), SB.niter_inner, SB.niter_solver)
fig, ax = plt.subplots()
ax.plot(time_axis, x.plot(), 'b', lw=2, label='true model')
ax.plot(time_axis, problemSB.model.plot(), 'r',  label='SB')
ax.legend(loc='upper left')
ax.set_ylim(-1., 1.), ax.set_xlim(*xlim)
ax.set_xlabel(xlbl), ax.set_ylabel("Amplitude")

axins1 = ax.inset_axes([0.42, 0.55, 0.1, 0.4])
axins1.plot(time_axis, x.plot(), 'b', lw=2)
axins1.plot(time_axis, problemSB.model.plot(), 'r')
axins1.set_xlim(0.76, 0.8)
axins1.set_ylim(-.1, .1)
axins1.set_xticklabels('')
axins1.set_yticklabels('') 
ax.indicate_inset_zoom(axins1)

axins2 = ax.inset_axes([0.55, 0.55, 0.1, 0.4])
axins2.plot(time_axis, x.plot(), 'b', lw=2)
axins2.plot(time_axis, problemSB.model.plot(), 'r')
axins2.set_xlim(1.51, 1.59)
axins2.set_ylim(-.1, .1)
axins2.set_xticklabels('')
axins2.set_yticklabels('') 
ax.indicate_inset_zoom(axins2)

axins3 = ax.inset_axes([0.49, 0.05, 0.1, 0.4])
axins3.plot(time_axis, x.plot(), 'b', lw=2)
axins3.plot(time_axis, problemSB.model.plot(), 'r')
axins3.set_xlim(1.0, 1.2)
axins3.set_ylim(-.1, .1)
axins3.set_xticklabels('')
axins3.set_yticklabels('') 
ax.indicate_inset_zoom(axins3)

plt.suptitle(r'Split-Bregman %s, $\varepsilon=%.e$' % (its, problemSB.eps))
plt.show()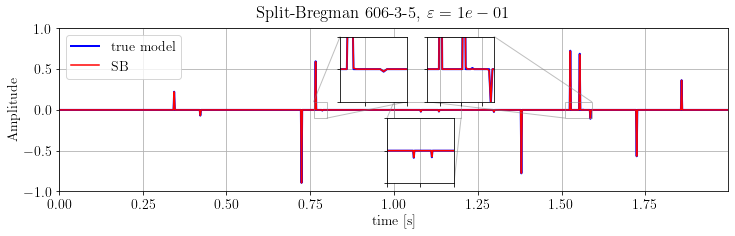
<Figure size 864x216 with 1 Axes>
fig, ax = plt.subplots()
ax.semilogy(time_axis, np.abs(x.plot()), 'b', label="true model")
ax.semilogy(time_axis, np.abs(problemSB.model.plot()), 'r', label="SB")
ax.set_xlim(*xlim), ax.set_ylim(1e-8, 1)
ax.legend(loc='upper left')
ax.set_xlabel(xlbl), ax.set_ylabel("Amplitude")

plt.suptitle(r'Split-Bregman %s, $\varepsilon=%.e$' % (its, problemSB.eps))
plt.show()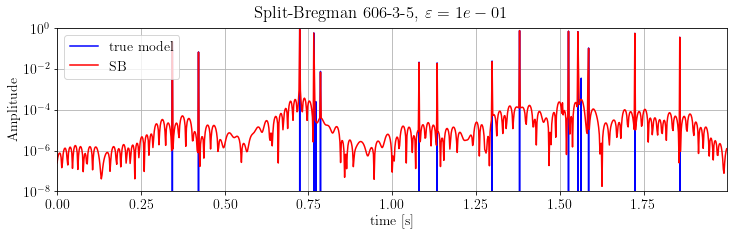
<Figure size 864x216 with 1 Axes>

The results is much better than FISTA output: the dynamics is almost-perfectly recovered.

Example 2: 1D Velocity Deconvolution

Now we create a synthetic velocity profile and suppose to have recorded a smooth version of it. The deconvolution problem aims at recovering the sharp model, and this is done by using a Total Variation regularizer.

# create the true model
nx = 201
x = o.VectorNumpy((nx,), ax_info=[o.AxInfo(201, 0, 1, "depth [sample]")]).zero()
x[20:30] = 10.
x[50:75] = -5.
x[100:150] = 2.5
x[175:180] = 7.5

# instantiate the blurring operator
G = o.GaussianFilter(x, (2.,))

# simulate data
d = G * x
fig, ax = plt.subplots()
ax.plot(x.plot(), 'k',  label='model')
ax.plot(d.plot(), 'b',  label='data')
ax.autoscale(enable=True, axis='x', tight=True)
ax.set_ylim(-6, 12)
plt.legend(loc="upper center")
ax.set_xlabel(x.ax_info[0].l), ax.set_ylabel("Amplitude")
plt.tight_layout(pad=.5)
plt.show()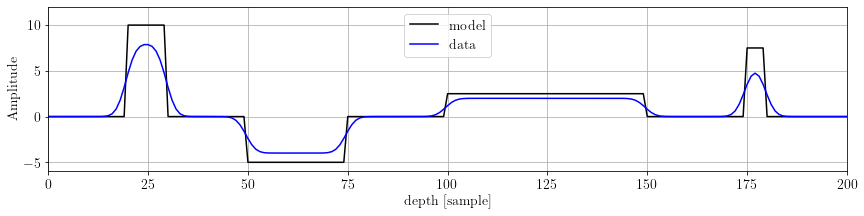
<Figure size 864x216 with 1 Axes>

As we can see, the model presents some flat regions. Let's have a look to its first derivative:

D = o.FirstDerivative(x, stencil='forward')
Dx = D * x
fig, ax = plt.subplots()
ax.plot(x.plot(), 'k',  label='model')
ax.stem(Dx.plot(), label='gradient', basefmt=':', use_line_collection=True)
ax.set_ylim(-12, 12)
ax.autoscale(enable=True, axis='x', tight=True)
plt.legend(loc="upper center")
ax.set_xlabel("Depth"), ax.set_ylabel("Amplitude")
plt.tight_layout(pad=.5)
plt.show()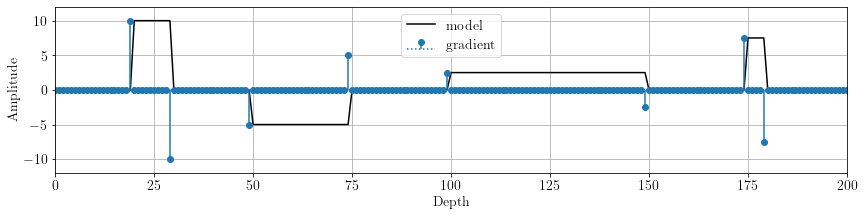
<Figure size 864x216 with 1 Axes>

The model derivative is sparse! We can set up a SplitBregman solver:

problem = o.GeneralizedLasso(x.clone().zero(), d, G, reg=D, eps=.1)

SB = o.SplitBregman(o.BasicStopper(200), niter_inner=3, niter_solver=10,
                           linear_solver='LSQR', breg_weight=1., warm_start=True)
SB.setDefaults(save_obj=True, save_model=True)

SB.run(problem, verbose=False, inner_verbose=False)
its = "%d-%d-%d" % (len(SB.obj), SB.niter_inner, SB.niter_solver)

fig, ax = plt.subplots()
ax.plot(x.plot(), 'b', lw=2, label="true model")
ax.plot(problem.model.plot(), 'r', label="SB")
ax.legend(loc="upper center")
ax.set_ylim(-6, 12)
ax.autoscale(enable=True, axis='x', tight=True)
ax.set_xlabel(x.ax_info[0].l), ax.set_ylabel("Amplitude")

plt.suptitle(r'Split-Bregman %s, $\varepsilon=%.e$' % (its, problem.eps))
plt.show()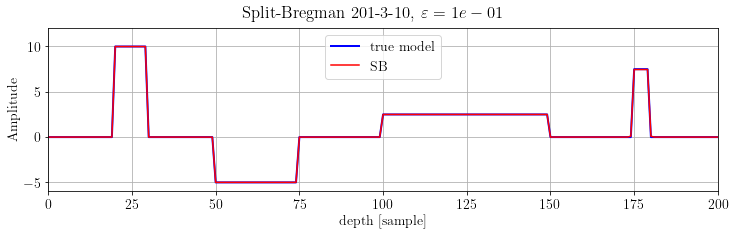
<Figure size 864x216 with 1 Axes>

Let's check the convergence:

fig, ax = plt.subplots()
ax.semilogy(SB.obj / SB.obj[0], 'k', lw=2, label='Obj')
ax.semilogy(SB.obj_terms[:, 0] / SB.obj[0], 'b--', label=r"$0.5 \Vert \mathbf{Gx-d} \Vert_2^2$")
ax.semilogy(SB.obj_terms[:, 1] / SB.obj[0], 'r--', label=r"$\varepsilon \Vert \mathbf{Dx}\Vert_1$")
ax.set_ylim(1e-7, 1), ax.set_xlim(0, SB.stopper.niter)
ax.set_xlabel("Iterations"), ax.set_ylabel("Amplitude")
ax.legend(loc="right")

plt.suptitle(r'Split-Bregman %s, $\varepsilon=%.e$' % (its, problem.eps))
plt.show()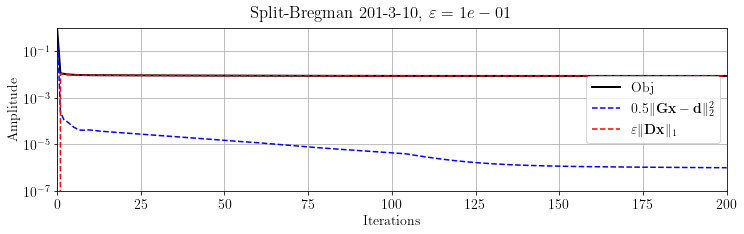
<Figure size 864x216 with 1 Axes>

We can see that the L1 term reaches its final value after few iterations. Let's see the inverted model after 2 iterations:

fig, ax = plt.subplots()
ax.plot(x.plot(), 'b', lw=2, label="true model")
ax.plot(SB.model[2].plot(), 'r', label="SB")
ax.legend(loc="upper center")
ax.set_ylim(-6, 12)
ax.autoscale(enable=True, axis='x', tight=True)
ax.set_xlabel(x.ax_info[0].l), ax.set_ylabel("Amplitude")

plt.suptitle(r'Split-Bregman %s after 2, $\varepsilon=%.e$' % (its, problem.eps))
plt.show()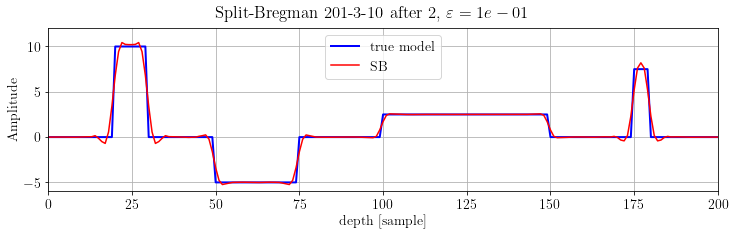
<Figure size 864x216 with 1 Axes>

Just for comparison, let's solve the problem with CG and FISTA.

problemCG = o.LeastSquares(x.clone().zero(), d, G)
CG = o.CG(o.BasicStopper(1000))
CG.setDefaults(save_obj=True)
CG.run(problemCG, verbose=False)

fig, ax = plt.subplots()
ax.plot(x.plot(), 'b', lw=2, label="true model")
ax.plot(problemCG.model.plot(), 'r', label="CG")
ax.legend(loc="upper center")
ax.set_ylim(-6, 12)
ax.autoscale(enable=True, axis='x', tight=True)
ax.set_xlabel(x.ax_info[0].l), ax.set_ylabel("Amplitude")

plt.suptitle('Conjugate Gradient, %d it' % len(CG.obj))
plt.show()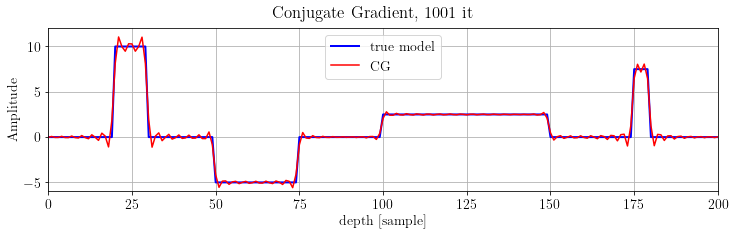
<Figure size 864x216 with 1 Axes>
# compute maximum eigenvalue
maxeig = G.powerMethod()
print('FISTA α=%.6e' % (1/(maxeig**2)))
problemFISTA = o.Lasso(x.clone().zero(), d, G, lambda_value=.1, op_norm=maxeig**2)
FISTA = o.ISTA(o.BasicStopper(1000), fast=True)
FISTA.setDefaults(save_obj=True)
FISTA.run(problemFISTA, verbose=False)

fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(x.plot(), 'b', lw=2, label="true model")
ax.plot(problemFISTA.model.plot(), 'r', label="FISTA")

ax.legend(loc="upper center")
ax.set_ylim(-6, 12)
ax.autoscale(enable=True, axis='x', tight=True)
ax.set_xlabel(x.ax_info[0].l), ax.set_ylabel("Amplitude")

plt.suptitle(r'Fast ISTA, $\lambda=$%.e, %d it' % (problemFISTA.lambda_value, len(FISTA.obj)))
plt.show()
FISTA α=1.570806e+00
<Figure size 864x216 with 1 Axes>

Example 3: 2D Phantom Deconvolution

In this example we reconstruct a phantom CT image starting from a blurred acquisition. Again, we regularize the inversion by imposing the first derivative to be sparse

# model
x = o.VectorNumpy(np.load('./data/shepp_logan_phantom.npy').astype(np.float32)).scale(1 / 255.)

# operator
G = o.GaussianFilter(x, (3.,3.))

# data
d = G * x
fig, ax = plt.subplots(1, 2, figsize=(11,4))
ax[0].imshow(x.plot(), cmap='bone', clim=(0,1))
ax[0].grid(False)
ax[0].set_title('Model')
ax[1].imshow(d.plot(), cmap='bone', clim=(0,1))
ax[1].grid(False)
ax[1].set_title('Data')
plt.show()
<Figure size 792x288 with 2 Axes>

Problem and solver:

D = o.Gradient(x)
Dx = D * x

fig, ax = plt.subplots(1, 2, figsize=(11,4))
ax[0].imshow(Dx.vecs[1].plot(), cmap='bone')
ax[0].grid(False)
ax[0].set_title(r'$\nabla_h(x)$')
ax[1].imshow(Dx.vecs[0].plot(), cmap='bone')
ax[1].grid(False)
ax[1].set_title(r'$\nabla_v(x)$')
plt.show()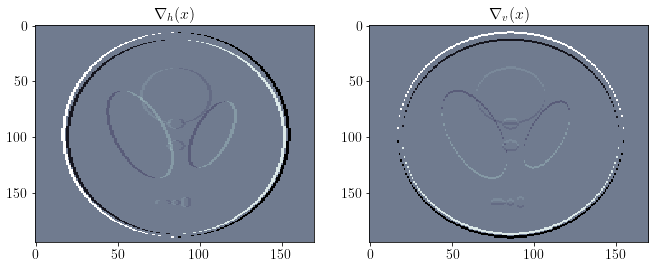
<Figure size 792x288 with 2 Axes>

Just for comparison, let's solve the problem with CG.

problemCG = o.LeastSquares(x.clone().zero(), d, G)
CG = o.CG(o.BasicStopper(1000))
CG.setDefaults(save_obj=True)
CG.run(problemCG, verbose=False)
fig, ax = plt.subplots(1, 2, figsize=(11,4))
ax[0].imshow(x.plot(), cmap='bone', clim=(0,1))
ax[0].grid(False)
ax[0].set_title('Model')
ax[1].imshow(problemCG.model.plot(), cmap='bone', clim=(0,1))
ax[1].grid(False)
ax[1].set_title('Conjugate Gradient, %d it' % len(CG.obj))
plt.show()
<Figure size 792x288 with 2 Axes>

See the ringing effect there? Let's remove it by means of a regularizer!

problemSB = o.GeneralizedLasso(x.clone().zero(), d, G, reg=D, eps=1e-3)
SB = o.SplitBregman(o.BasicStopper(niter=200), niter_inner=3, niter_solver=10,
                           linear_solver='LSQR', breg_weight=1., warm_start=True)
SB.setDefaults(save_obj=True)
SB.run(problemSB, verbose=False, inner_verbose=False)
its = "%d-%d-%d" % (len(SB.obj), SB.niter_inner, SB.niter_solver)

fig, ax = plt.subplots(1, 2, figsize=(11,4))
ax[0].imshow(x.plot(), cmap='bone', clim=(0,1))
ax[0].grid(False)
ax[0].set_title('Model')
ax[1].imshow(problemSB.model.plot(), cmap='bone', clim=(0,1))
ax[1].grid(False)
ax[1].set_title(r'SB %s, $\varepsilon=%.e$' % (its, problemSB.eps))
plt.show()
<Figure size 792x288 with 2 Axes>

Again, let's evaluate the objective function terms

fig, ax = plt.subplots()
ax.semilogy(SB.obj / SB.obj[0], 'k', lw=2, label='Obj')
ax.semilogy(SB.obj_terms[:, 0] / SB.obj[0], 'b--', label=r"$0.5 \Vert \mathbf{Gx-d} \Vert_2^2$")
ax.semilogy(SB.obj_terms[:, 1] / SB.obj[0], 'r--', label=r"$\varepsilon \Vert \mathbf{Dx}\Vert_1$")
ax.set_ylim(1e-8, 1), ax.set_xlim(0, SB.stopper.niter)
ax.set_xlabel("Iterations")
ax.legend(loc="right")

plt.suptitle(r'Split-Bregman %s, $\varepsilon=%.e$' % (its, problem.eps))
plt.show()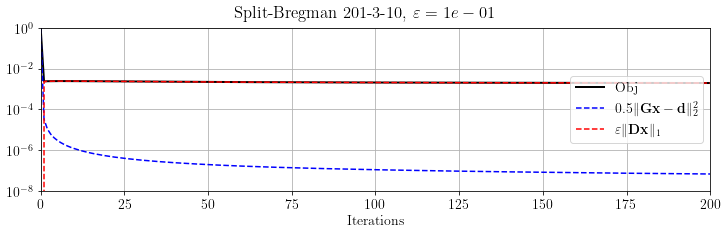
<Figure size 864x216 with 1 Axes>
References
  1. Goldstein, T., & Osher, S. (2009). The Split Bregman Method for L1-Regularized Problems. SIAM Journal on Imaging Sciences, 2(2), 323–343. 10.1137/080725891
  2. Beck, A., & Teboulle, M. (2009). A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM Journal on Imaging Sciences, 2(1), 183–202. 10.1137/080716542
Notebooks
Simple quadratic problems
Notebooks
TorchVector: going on GPU