Testing non-linear solvers on the Rosenbrock function¶

@Author: Ettore Biondi - ebiondi@caltech.edu

Problem definition¶

In this notebook we show how to set a user-defined objective function and minimize it using different solvers. The function understudy is the well-known convex Rosenbrock function. Its analytical form for the 2D case takes the follwing form:

\begin{equation} \phi(x,y) = (1-x)^2 + 100 (y-x^2)^2, \end{equation}

(1)

in which the unique global minimum is at $x=y=1$ . The global minimum is inside a long, narrow, parabolic-shaped flat valley. To find the valley is trivial. To converge to the global minimum, however, is difficult. Hence, this function represents a good testing case for any non-linear optimization scheme.

import numpy as np
import occamypy as o

# Plotting
from matplotlib import rcParams
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib.pyplot as plt
rcParams.update({
    'image.cmap'     : 'jet',
    'image.aspect'   : 'auto',
    'image.interpolation': None,
    'axes.grid'      : False,
    'figure.figsize' : (10, 6),
    'savefig.dpi'    : 300,
    'axes.labelsize' : 14,
    'axes.titlesize' : 16,
    'font.size'      : 14,
    'legend.fontsize': 14,
    'xtick.labelsize': 14,
    'ytick.labelsize': 14,
    'text.usetex'    : True,
    'font.family'    : 'serif',
    'font.serif'     : 'Latin Modern Roman',
})

WARNING! DATAPATH not found. The folder /tmp will be used to write binary files

/nas/home/fpicetti/miniconda3/envs/occd/lib/python3.10/site-packages/dask_jobqueue/core.py:20: FutureWarning: tmpfile is deprecated and will be removed in a future release. Please use dask.utils.tmpfile instead.
  from distributed.utils import tmpfile

Let's first define the problem object. Our model vector is going to be $\mathbf{m} = [x \,, \, y]^T$ . Since the libary assumes that the objective function is written in terms of some residual vector (i.e., $\phi(\mathbf{r}(\mathbf{m}))$ , we will create a vector containing objective function as a single scalar value.

class Rosenbrock(o.Problem):
    """
    Rosenbrock function inverse problem
    f(x,y) = (1 - x)^2 + 100*(y -x^2)^2
    m = [x y]'
    res = objective function value
    """

    def __init__(self, x_initial, y_initial, minBound=None, maxBound=None):
        """Constructor of linear problem"""
        #Setting the bounds (if any)
        super(Rosenbrock, self).__init__(model=o.VectorNumpy(np.array((x_initial, y_initial))),
                                         data=o.VectorNumpy((1,)),
                                         minBound=minBound, maxBound=maxBound)
        
        #Gradient vector
        self.grad = self.pert_model.clone()
        
        #Setting default variables
        self.setDefaults()
        self.linear = False
        return

    def obj_func(self, model):
        m = model.getNdArray()
        obj = self.res.arr[0]
        return obj

    def res_func(self, model):
        m = model.getNdArray()
        self.res[0] = (1.0 - m[0])*(1.0 - m[0]) + 100.0 * (m[1] - m[0]*m[0]) * (m[1] - m[0]*m[0])
        return self.res

    def grad_func(self, model, residual):
        m = model.getNdArray()
        self.grad[0] = - 2.0 * (1.0 - m[0]) - 400.0 * m[0] * (m[1] - m[0]*m[0])
        self.grad[1] = 200.0 * (m[1] - m[0]*m[0])
        return self.grad

    def pert_res_func(self, model, pert_model):
        m = model.getNdArray()
        dm = pert_model.getNdArray()
        self.pert_res.arr[0] = (- 2.0 * (1.0 - m[0]) - 400.0 * m[0] * (m[1] - m[0]*m[0]))* dm[0] + (200.0 * (m[1] - m[0]*m[0])) * dm[1]
        return self.pert_res

Instantiation of the inverse problem and of the various solvers¶

# Starting point for all the optimization problem
x_init = -1.0
y_init = -1.0
# Testing solver on Rosenbrock function
Ros_prob = Rosenbrock(x_init, y_init)

Before running any inversion, let's compute the objective function for different values of $x$ and $y$ . This step will be useful when we want to plot the optimization path taken by the various tested algorithms.

#Computing the objective function for plotting
x_samples = np.linspace(-1.5,  1.5, 1000)
y_samples = np.linspace(   3, -1.5, 1000)

obj_ros = o.VectorNumpy((x_samples.size, y_samples.size))
model_test = o.VectorNumpy((2,))

for ix, x_value in enumerate(x_samples):
    for iy, y_value in enumerate(y_samples):
        model_test[0]  = x_value
        model_test[1]  = y_value
        obj_ros[ix, iy] = Ros_prob.get_obj(model_test)

First we test a non-linear conjugate-gradient method in which a parabolic stepper with three-point interpolation is used.

niter = 1000
Stop  = o.BasicStopper(niter=niter, tolr=1e-32, tolg=1e-32)
NLCGsolver = o.NLCG(Stop)
Ros_prob = Rosenbrock(x_init, y_init) #Resetting the problem
NLCGsolver.setDefaults(save_obj=True, save_model=True)
NLCGsolver.run(Ros_prob,verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(NLCGsolver.model)):
    x_smpld.append(NLCGsolver.model[i][0])
    y_smpld.append(NLCGsolver.model[i][1])

##########################################################################################
            Nonlinear CG Solver 
    Restart folder: /tmp/restart_2022-04-22T01-49-05.870101/
    Conjugate method used: FR
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 4.01e+01, rnorm = 4.01e+01, gnorm = 1.33e+02, feval = 00004, geval = 0002
iter = 0002, obj = 1.75e+00, rnorm = 1.75e+00, gnorm = 1.87e+01, feval = 00007, geval = 0003
iter = 0003, obj = 8.70e-01, rnorm = 8.70e-01, gnorm = 1.88e+00, feval = 00010, geval = 0004
iter = 0004, obj = 8.40e-01, rnorm = 8.40e-01, gnorm = 1.81e+00, feval = 00013, geval = 0005
iter = 0005, obj = 7.38e-01, rnorm = 7.38e-01, gnorm = 2.27e+00, feval = 00016, geval = 0006
iter = 0006, obj = 5.41e-01, rnorm = 5.41e-01, gnorm = 4.40e+00, feval = 00019, geval = 0007
iter = 0007, obj = 4.83e-01, rnorm = 4.83e-01, gnorm = 6.47e+00, feval = 00025, geval = 0008
iter = 0008, obj = 4.42e-01, rnorm = 4.42e-01, gnorm = 8.56e+00, feval = 00028, geval = 0009
iter = 0009, obj = 4.17e-01, rnorm = 4.17e-01, gnorm = 1.02e+01, feval = 00031, geval = 0010
iter = 0010, obj = 3.92e-01, rnorm = 3.92e-01, gnorm = 1.15e+01, feval = 00034, geval = 0011
iter = 0011, obj = 3.60e-01, rnorm = 3.60e-01, gnorm = 1.29e+01, feval = 00037, geval = 0012
iter = 0012, obj = 3.30e-01, rnorm = 3.30e-01, gnorm = 1.40e+01, feval = 00040, geval = 0013
iter = 0013, obj = 2.93e-01, rnorm = 2.93e-01, gnorm = 1.50e+01, feval = 00043, geval = 0014
iter = 0014, obj = 2.53e-01, rnorm = 2.53e-01, gnorm = 1.58e+01, feval = 00046, geval = 0015
iter = 0015, obj = 2.11e-01, rnorm = 2.11e-01, gnorm = 1.62e+01, feval = 00049, geval = 0016
iter = 0016, obj = 1.60e-01, rnorm = 1.60e-01, gnorm = 1.59e+01, feval = 00052, geval = 0017
iter = 0017, obj = 9.93e-02, rnorm = 9.93e-02, gnorm = 1.40e+01, feval = 00055, geval = 0018
iter = 0018, obj = 3.16e-02, rnorm = 3.16e-02, gnorm = 7.52e+00, feval = 00058, geval = 0019
iter = 0019, obj = 1.21e-02, rnorm = 1.21e-02, gnorm = 7.15e-01, feval = 00061, geval = 0020
iter = 0020, obj = 1.19e-02, rnorm = 1.19e-02, gnorm = 1.17e-01, feval = 00064, geval = 0021
iter = 0021, obj = 1.19e-02, rnorm = 1.19e-02, gnorm = 1.12e-01, feval = 00067, geval = 0022
iter = 0022, obj = 1.18e-02, rnorm = 1.18e-02, gnorm = 6.58e-01, feval = 00070, geval = 0023
iter = 0023, obj = 5.43e-04, rnorm = 5.43e-04, gnorm = 1.03e+00, feval = 00073, geval = 0024
iter = 0024, obj = 1.37e-04, rnorm = 1.37e-04, gnorm = 1.99e-01, feval = 00081, geval = 0025
iter = 0025, obj = 1.21e-04, rnorm = 1.21e-04, gnorm = 2.40e-02, feval = 00084, geval = 0026
iter = 0026, obj = 1.21e-04, rnorm = 1.21e-04, gnorm = 9.97e-03, feval = 00087, geval = 0027
iter = 0027, obj = 1.20e-04, rnorm = 1.20e-04, gnorm = 3.33e-02, feval = 00090, geval = 0028
iter = 0028, obj = 9.35e-05, rnorm = 9.35e-05, gnorm = 2.26e-01, feval = 00093, geval = 0029
iter = 0029, obj = 7.61e-06, rnorm = 7.61e-06, gnorm = 2.50e-03, feval = 00099, geval = 0030
iter = 0030, obj = 7.56e-06, rnorm = 7.56e-06, gnorm = 9.80e-03, feval = 00102, geval = 0031
iter = 0031, obj = 6.89e-06, rnorm = 6.89e-06, gnorm = 2.64e-02, feval = 00105, geval = 0032
iter = 0032, obj = 3.86e-06, rnorm = 3.86e-06, gnorm = 4.19e-02, feval = 00108, geval = 0033
iter = 0033, obj = 1.30e-06, rnorm = 1.30e-06, gnorm = 2.20e-02, feval = 00111, geval = 0034
iter = 0034, obj = 8.42e-07, rnorm = 8.42e-07, gnorm = 7.67e-03, feval = 00114, geval = 0035
iter = 0035, obj = 7.89e-07, rnorm = 7.89e-07, gnorm = 2.78e-03, feval = 00117, geval = 0036
iter = 0036, obj = 7.81e-07, rnorm = 7.81e-07, gnorm = 1.57e-03, feval = 00120, geval = 0037
iter = 0037, obj = 7.76e-07, rnorm = 7.76e-07, gnorm = 2.10e-03, feval = 00123, geval = 0038
iter = 0038, obj = 7.51e-07, rnorm = 7.51e-07, gnorm = 5.12e-03, feval = 00126, geval = 0039
iter = 0039, obj = 5.92e-07, rnorm = 5.92e-07, gnorm = 1.17e-02, feval = 00129, geval = 0040
iter = 0040, obj = 2.40e-07, rnorm = 2.40e-07, gnorm = 1.12e-02, feval = 00132, geval = 0041
iter = 0041, obj = 1.03e-07, rnorm = 1.03e-07, gnorm = 4.59e-03, feval = 00135, geval = 0042
iter = 0042, obj = 8.37e-08, rnorm = 8.37e-08, gnorm = 1.58e-03, feval = 00138, geval = 0043
iter = 0043, obj = 8.14e-08, rnorm = 8.14e-08, gnorm = 6.45e-04, feval = 00141, geval = 0044
iter = 0044, obj = 8.08e-08, rnorm = 8.08e-08, gnorm = 5.14e-04, feval = 00144, geval = 0045
iter = 0045, obj = 7.99e-08, rnorm = 7.99e-08, gnorm = 9.49e-04, feval = 00147, geval = 0046
iter = 0046, obj = 7.40e-08, rnorm = 7.40e-08, gnorm = 2.46e-03, feval = 00150, geval = 0047
iter = 0047, obj = 4.59e-08, rnorm = 4.59e-08, gnorm = 4.28e-03, feval = 00153, geval = 0048
iter = 0048, obj = 1.59e-08, rnorm = 1.59e-08, gnorm = 2.61e-03, feval = 00156, geval = 0049
iter = 0049, obj = 9.27e-09, rnorm = 9.27e-09, gnorm = 9.41e-04, feval = 00159, geval = 0050
iter = 0050, obj = 8.47e-09, rnorm = 8.47e-09, gnorm = 3.31e-04, feval = 00162, geval = 0051
iter = 0051, obj = 8.37e-09, rnorm = 8.37e-09, gnorm = 1.68e-04, feval = 00165, geval = 0052
iter = 0052, obj = 8.31e-09, rnorm = 8.31e-09, gnorm = 1.96e-04, feval = 00168, geval = 0053
iter = 0053, obj = 8.11e-09, rnorm = 8.11e-09, gnorm = 4.58e-04, feval = 00171, geval = 0054
iter = 0054, obj = 6.77e-09, rnorm = 6.77e-09, gnorm = 1.11e-03, feval = 00174, geval = 0055
iter = 0055, obj = 3.03e-09, rnorm = 3.03e-09, gnorm = 1.25e-03, feval = 00177, geval = 0056
iter = 0056, obj = 1.17e-09, rnorm = 1.17e-09, gnorm = 5.50e-04, feval = 00180, geval = 0057
iter = 0057, obj = 8.97e-10, rnorm = 8.97e-10, gnorm = 1.89e-04, feval = 00183, geval = 0058
iter = 0058, obj = 8.64e-10, rnorm = 8.64e-10, gnorm = 7.30e-05, feval = 00186, geval = 0059
iter = 0059, obj = 8.58e-10, rnorm = 8.58e-10, gnorm = 5.15e-05, feval = 00189, geval = 0060
iter = 0060, obj = 8.50e-10, rnorm = 8.50e-10, gnorm = 8.67e-05, feval = 00192, geval = 0061
iter = 0061, obj = 8.02e-10, rnorm = 8.02e-10, gnorm = 2.24e-04, feval = 00195, geval = 0062
iter = 0062, obj = 5.41e-10, rnorm = 5.41e-10, gnorm = 4.34e-04, feval = 00198, geval = 0063
iter = 0063, obj = 1.90e-10, rnorm = 1.90e-10, gnorm = 3.00e-04, feval = 00201, geval = 0064
iter = 0064, obj = 1.01e-10, rnorm = 1.01e-10, gnorm = 1.11e-04, feval = 00204, geval = 0065
iter = 0065, obj = 9.00e-11, rnorm = 9.00e-11, gnorm = 3.85e-05, feval = 00207, geval = 0066
iter = 0066, obj = 8.85e-11, rnorm = 8.85e-11, gnorm = 1.81e-05, feval = 00210, geval = 0067
iter = 0067, obj = 8.80e-11, rnorm = 8.80e-11, gnorm = 1.89e-05, feval = 00213, geval = 0068
iter = 0068, obj = 8.63e-11, rnorm = 8.63e-11, gnorm = 4.17e-05, feval = 00216, geval = 0069
iter = 0069, obj = 7.49e-11, rnorm = 7.49e-11, gnorm = 1.05e-04, feval = 00219, geval = 0070
iter = 0070, obj = 3.68e-11, rnorm = 3.68e-11, gnorm = 1.35e-04, feval = 00222, geval = 0071
iter = 0071, obj = 1.34e-11, rnorm = 1.34e-11, gnorm = 6.41e-05, feval = 00225, geval = 0072
iter = 0072, obj = 9.61e-12, rnorm = 9.61e-12, gnorm = 2.22e-05, feval = 00228, geval = 0073
iter = 0073, obj = 9.16e-12, rnorm = 9.16e-12, gnorm = 8.27e-06, feval = 00231, geval = 0074
iter = 0074, obj = 9.08e-12, rnorm = 9.08e-12, gnorm = 5.27e-06, feval = 00234, geval = 0075
iter = 0075, obj = 9.01e-12, rnorm = 9.01e-12, gnorm = 8.05e-06, feval = 00237, geval = 0076
iter = 0076, obj = 8.61e-12, rnorm = 8.61e-12, gnorm = 2.05e-05, feval = 00240, geval = 0077
iter = 0077, obj = 6.26e-12, rnorm = 6.26e-12, gnorm = 4.31e-05, feval = 00243, geval = 0078
iter = 0078, obj = 2.30e-12, rnorm = 2.30e-12, gnorm = 3.40e-05, feval = 00246, geval = 0079
iter = 0079, obj = 1.11e-12, rnorm = 1.11e-12, gnorm = 1.30e-05, feval = 00249, geval = 0080
iter = 0080, obj = 9.57e-13, rnorm = 9.57e-13, gnorm = 4.49e-06, feval = 00252, geval = 0081
iter = 0081, obj = 9.38e-13, rnorm = 9.38e-13, gnorm = 1.97e-06, feval = 00255, geval = 0082
iter = 0082, obj = 9.32e-13, rnorm = 9.32e-13, gnorm = 1.84e-06, feval = 00258, geval = 0083
iter = 0083, obj = 9.18e-13, rnorm = 9.18e-13, gnorm = 3.80e-06, feval = 00261, geval = 0084
iter = 0084, obj = 8.22e-13, rnorm = 8.22e-13, gnorm = 9.78e-06, feval = 00264, geval = 0085
iter = 0085, obj = 4.44e-13, rnorm = 4.44e-13, gnorm = 1.44e-05, feval = 00267, geval = 0086
iter = 0086, obj = 1.55e-13, rnorm = 1.55e-13, gnorm = 7.46e-06, feval = 00270, geval = 0087
iter = 0087, obj = 1.03e-13, rnorm = 1.03e-13, gnorm = 2.61e-06, feval = 00273, geval = 0088
iter = 0088, obj = 9.71e-14, rnorm = 9.71e-14, gnorm = 9.47e-07, feval = 00276, geval = 0089
iter = 0089, obj = 9.62e-14, rnorm = 9.62e-14, gnorm = 5.47e-07, feval = 00279, geval = 0090
iter = 0090, obj = 9.55e-14, rnorm = 9.55e-14, gnorm = 7.53e-07, feval = 00282, geval = 0091
iter = 0091, obj = 9.22e-14, rnorm = 9.22e-14, gnorm = 1.87e-06, feval = 00285, geval = 0092
iter = 0092, obj = 7.13e-14, rnorm = 7.13e-14, gnorm = 4.21e-06, feval = 00288, geval = 0093
iter = 0093, obj = 2.81e-14, rnorm = 2.81e-14, gnorm = 3.82e-06, feval = 00291, geval = 0094
iter = 0094, obj = 1.23e-14, rnorm = 1.23e-14, gnorm = 1.53e-06, feval = 00294, geval = 0095
iter = 0095, obj = 1.02e-14, rnorm = 1.02e-14, gnorm = 5.25e-07, feval = 00297, geval = 0096
iter = 0096, obj = 9.93e-15, rnorm = 9.93e-15, gnorm = 2.18e-07, feval = 00300, geval = 0097
iter = 0097, obj = 9.87e-15, rnorm = 9.87e-15, gnorm = 1.81e-07, feval = 00303, geval = 0098
iter = 0098, obj = 9.75e-15, rnorm = 9.75e-15, gnorm = 3.48e-07, feval = 00306, geval = 0099
iter = 0099, obj = 8.95e-15, rnorm = 8.95e-15, gnorm = 9.04e-07, feval = 00309, geval = 0100
iter = 0100, obj = 5.31e-15, rnorm = 5.31e-15, gnorm = 1.50e-06, feval = 00312, geval = 0101
iter = 0101, obj = 1.83e-15, rnorm = 1.83e-15, gnorm = 8.63e-07, feval = 00315, geval = 0102
iter = 0102, obj = 1.12e-15, rnorm = 1.12e-15, gnorm = 3.07e-07, feval = 00318, geval = 0103
iter = 0103, obj = 1.03e-15, rnorm = 1.03e-15, gnorm = 1.09e-07, feval = 00321, geval = 0104
iter = 0104, obj = 1.02e-15, rnorm = 1.02e-15, gnorm = 5.77e-08, feval = 00324, geval = 0105
iter = 0105, obj = 1.01e-15, rnorm = 1.01e-15, gnorm = 7.12e-08, feval = 00327, geval = 0106
iter = 0106, obj = 9.84e-16, rnorm = 9.84e-16, gnorm = 1.70e-07, feval = 00330, geval = 0107
iter = 0107, obj = 8.03e-16, rnorm = 8.03e-16, gnorm = 4.04e-07, feval = 00333, geval = 0108
iter = 0108, obj = 3.43e-16, rnorm = 3.43e-16, gnorm = 4.23e-07, feval = 00336, geval = 0109
iter = 0109, obj = 1.38e-16, rnorm = 1.38e-16, gnorm = 1.80e-07, feval = 00339, geval = 0110
iter = 0110, obj = 1.09e-16, rnorm = 1.09e-16, gnorm = 6.16e-08, feval = 00342, geval = 0111
iter = 0111, obj = 1.05e-16, rnorm = 1.05e-16, gnorm = 2.43e-08, feval = 00345, geval = 0112
iter = 0112, obj = 1.05e-16, rnorm = 1.05e-16, gnorm = 1.81e-08, feval = 00348, geval = 0113
iter = 0113, obj = 1.03e-16, rnorm = 1.03e-16, gnorm = 3.20e-08, feval = 00351, geval = 0114
iter = 0114, obj = 9.68e-17, rnorm = 9.68e-17, gnorm = 8.31e-08, feval = 00354, geval = 0115
iter = 0115, obj = 6.27e-17, rnorm = 6.27e-17, gnorm = 1.53e-07, feval = 00357, geval = 0116
iter = 0116, obj = 2.18e-17, rnorm = 2.18e-17, gnorm = 9.92e-08, feval = 00360, geval = 0117
iter = 0117, obj = 1.21e-17, rnorm = 1.21e-17, gnorm = 3.62e-08, feval = 00363, geval = 0118
iter = 0118, obj = 1.09e-17, rnorm = 1.09e-17, gnorm = 1.26e-08, feval = 00366, geval = 0119
iter = 0119, obj = 1.08e-17, rnorm = 1.08e-17, gnorm = 6.16e-09, feval = 00369, geval = 0120
iter = 0120, obj = 1.07e-17, rnorm = 1.07e-17, gnorm = 6.80e-09, feval = 00372, geval = 0121
iter = 0121, obj = 1.05e-17, rnorm = 1.05e-17, gnorm = 1.55e-08, feval = 00375, geval = 0122
iter = 0122, obj = 8.94e-18, rnorm = 8.94e-18, gnorm = 3.83e-08, feval = 00378, geval = 0123
iter = 0123, obj = 4.18e-18, rnorm = 4.18e-18, gnorm = 4.61e-08, feval = 00381, geval = 0124
iter = 0124, obj = 1.57e-18, rnorm = 1.57e-18, gnorm = 2.10e-08, feval = 00384, geval = 0125
iter = 0125, obj = 1.16e-18, rnorm = 1.16e-18, gnorm = 7.24e-09, feval = 00387, geval = 0126
iter = 0126, obj = 1.12e-18, rnorm = 1.12e-18, gnorm = 2.75e-09, feval = 00390, geval = 0127
iter = 0127, obj = 1.11e-18, rnorm = 1.11e-18, gnorm = 1.84e-09, feval = 00393, geval = 0128
iter = 0128, obj = 1.10e-18, rnorm = 1.10e-18, gnorm = 2.96e-09, feval = 00396, geval = 0129
iter = 0129, obj = 1.04e-18, rnorm = 1.04e-18, gnorm = 7.60e-09, feval = 00399, geval = 0130
iter = 0130, obj = 7.30e-19, rnorm = 7.30e-19, gnorm = 1.54e-08, feval = 00402, geval = 0131
iter = 0131, obj = 2.62e-19, rnorm = 2.62e-19, gnorm = 1.13e-08, feval = 00405, geval = 0132
iter = 0132, obj = 1.33e-19, rnorm = 1.33e-19, gnorm = 4.26e-09, feval = 00408, geval = 0133
iter = 0133, obj = 1.16e-19, rnorm = 1.16e-19, gnorm = 1.47e-09, feval = 00411, geval = 0134
iter = 0134, obj = 1.14e-19, rnorm = 1.14e-19, gnorm = 6.67e-10, feval = 00414, geval = 0135
iter = 0135, obj = 1.14e-19, rnorm = 1.14e-19, gnorm = 6.58e-10, feval = 00417, geval = 0136
iter = 0136, obj = 1.12e-19, rnorm = 1.12e-19, gnorm = 1.41e-09, feval = 00420, geval = 0137
iter = 0137, obj = 9.85e-20, rnorm = 9.85e-20, gnorm = 3.59e-09, feval = 00423, geval = 0138
iter = 0138, obj = 5.07e-20, rnorm = 5.07e-20, gnorm = 4.95e-09, feval = 00426, geval = 0139
iter = 0139, obj = 1.80e-20, rnorm = 1.80e-20, gnorm = 2.45e-09, feval = 00429, geval = 0140
iter = 0140, obj = 1.25e-20, rnorm = 1.25e-20, gnorm = 8.51e-10, feval = 00432, geval = 0141
iter = 0141, obj = 1.18e-20, rnorm = 1.18e-20, gnorm = 3.12e-10, feval = 00435, geval = 0142
iter = 0142, obj = 1.17e-20, rnorm = 1.17e-20, gnorm = 1.90e-10, feval = 00438, geval = 0143
iter = 0143, obj = 1.16e-20, rnorm = 1.16e-20, gnorm = 2.75e-10, feval = 00441, geval = 0144
iter = 0144, obj = 1.12e-20, rnorm = 1.12e-20, gnorm = 6.94e-10, feval = 00444, geval = 0145
iter = 0145, obj = 8.36e-21, rnorm = 8.36e-21, gnorm = 1.52e-09, feval = 00447, geval = 0146
iter = 0146, obj = 3.15e-21, rnorm = 3.15e-21, gnorm = 1.27e-09, feval = 00450, geval = 0147
iter = 0147, obj = 1.45e-21, rnorm = 1.45e-21, gnorm = 4.96e-10, feval = 00453, geval = 0148
iter = 0148, obj = 1.23e-21, rnorm = 1.23e-21, gnorm = 1.70e-10, feval = 00456, geval = 0149
iter = 0149, obj = 1.20e-21, rnorm = 1.20e-21, gnorm = 7.24e-11, feval = 00459, geval = 0150
iter = 0150, obj = 1.19e-21, rnorm = 1.19e-21, gnorm = 6.43e-11, feval = 00462, geval = 0151
iter = 0151, obj = 1.18e-21, rnorm = 1.18e-21, gnorm = 1.29e-10, feval = 00465, geval = 0152
iter = 0152, obj = 1.07e-21, rnorm = 1.07e-21, gnorm = 3.36e-10, feval = 00468, geval = 0153
iter = 0153, obj = 5.95e-22, rnorm = 5.95e-22, gnorm = 5.19e-10, feval = 00471, geval = 0154
iter = 0154, obj = 2.04e-22, rnorm = 2.04e-22, gnorm = 2.79e-10, feval = 00474, geval = 0155
iter = 0155, obj = 1.32e-22, rnorm = 1.32e-22, gnorm = 9.74e-11, feval = 00477, geval = 0156
iter = 0156, obj = 1.23e-22, rnorm = 1.23e-22, gnorm = 3.47e-11, feval = 00480, geval = 0157
iter = 0157, obj = 1.22e-22, rnorm = 1.22e-22, gnorm = 1.94e-11, feval = 00483, geval = 0158
iter = 0158, obj = 1.21e-22, rnorm = 1.21e-22, gnorm = 2.63e-11, feval = 00486, geval = 0159
iter = 0159, obj = 1.17e-22, rnorm = 1.17e-22, gnorm = 6.59e-11, feval = 00489, geval = 0160
iter = 0160, obj = 9.12e-23, rnorm = 9.12e-23, gnorm = 1.49e-10, feval = 00492, geval = 0161
iter = 0161, obj = 3.56e-23, rnorm = 3.56e-23, gnorm = 1.37e-10, feval = 00495, geval = 0162
iter = 0162, obj = 1.53e-23, rnorm = 1.53e-23, gnorm = 5.44e-11, feval = 00498, geval = 0163
iter = 0163, obj = 1.27e-23, rnorm = 1.27e-23, gnorm = 1.84e-11, feval = 00501, geval = 0164
iter = 0164, obj = 1.23e-23, rnorm = 1.23e-23, gnorm = 7.57e-12, feval = 00504, geval = 0165
iter = 0165, obj = 1.23e-23, rnorm = 1.23e-23, gnorm = 6.38e-12, feval = 00507, geval = 0166
iter = 0166, obj = 1.21e-23, rnorm = 1.21e-23, gnorm = 1.25e-11, feval = 00510, geval = 0167
iter = 0167, obj = 1.11e-23, rnorm = 1.11e-23, gnorm = 3.26e-11, feval = 00513, geval = 0168
iter = 0168, obj = 6.38e-24, rnorm = 6.38e-24, gnorm = 5.34e-11, feval = 00516, geval = 0169
iter = 0169, obj = 2.13e-24, rnorm = 2.13e-24, gnorm = 2.91e-11, feval = 00519, geval = 0170
iter = 0170, obj = 1.33e-24, rnorm = 1.33e-24, gnorm = 1.00e-11, feval = 00522, geval = 0171
iter = 0171, obj = 1.24e-24, rnorm = 1.24e-24, gnorm = 4.20e-12, feval = 00525, geval = 0172
iter = 0172, obj = 1.23e-24, rnorm = 1.23e-24, gnorm = 2.04e-12, feval = 00528, geval = 0173
iter = 0173, obj = 1.22e-24, rnorm = 1.22e-24, gnorm = 2.23e-12, feval = 00531, geval = 0174
iter = 0174, obj = 1.19e-24, rnorm = 1.19e-24, gnorm = 5.22e-12, feval = 00534, geval = 0175
iter = 0175, obj = 1.04e-24, rnorm = 1.04e-24, gnorm = 1.18e-11, feval = 00537, geval = 0176
iter = 0176, obj = 4.99e-25, rnorm = 4.99e-25, gnorm = 1.62e-11, feval = 00540, geval = 0177
iter = 0177, obj = 1.66e-25, rnorm = 1.66e-25, gnorm = 7.50e-12, feval = 00543, geval = 0178
iter = 0178, obj = 1.16e-25, rnorm = 1.16e-25, gnorm = 2.61e-12, feval = 00546, geval = 0179
iter = 0179, obj = 1.10e-25, rnorm = 1.10e-25, gnorm = 9.47e-13, feval = 00549, geval = 0180
iter = 0180, obj = 1.09e-25, rnorm = 1.09e-25, gnorm = 5.72e-13, feval = 00552, geval = 0181
iter = 0181, obj = 1.08e-25, rnorm = 1.08e-25, gnorm = 6.73e-13, feval = 00554, geval = 0182
iter = 0182, obj = 1.06e-25, rnorm = 1.06e-25, gnorm = 1.21e-12, feval = 00557, geval = 0183
iter = 0183, obj = 9.54e-26, rnorm = 9.54e-26, gnorm = 2.95e-12, feval = 00560, geval = 0184
iter = 0184, obj = 4.86e-26, rnorm = 4.86e-26, gnorm = 5.21e-12, feval = 00563, geval = 0185
iter = 0185, obj = 9.88e-27, rnorm = 9.88e-27, gnorm = 2.23e-12, feval = 00566, geval = 0186
iter = 0186, obj = 5.89e-27, rnorm = 5.89e-27, gnorm = 6.36e-13, feval = 00569, geval = 0187
iter = 0187, obj = 5.55e-27, rnorm = 5.55e-27, gnorm = 9.34e-14, feval = 00572, geval = 0188
iter = 0188, obj = 5.53e-27, rnorm = 5.53e-27, gnorm = 1.49e-13, feval = 00574, geval = 0189
iter = 0189, obj = 5.40e-27, rnorm = 5.40e-27, gnorm = 1.47e-13, feval = 00577, geval = 0190
iter = 0190, obj = 5.35e-27, rnorm = 5.35e-27, gnorm = 1.80e-13, feval = 00580, geval = 0191
iter = 0191, obj = 5.16e-27, rnorm = 5.16e-27, gnorm = 2.77e-13, feval = 00582, geval = 0192
iter = 0192, obj = 4.91e-27, rnorm = 4.91e-27, gnorm = 4.27e-13, feval = 00585, geval = 0193
iter = 0193, obj = 3.99e-27, rnorm = 3.99e-27, gnorm = 1.39e-12, feval = 00588, geval = 0194
iter = 0194, obj = 1.09e-28, rnorm = 1.09e-28, gnorm = 4.42e-13, feval = 00591, geval = 0195
iter = 0195, obj = 3.08e-29, rnorm = 3.08e-29, gnorm = 1.41e-13, feval = 00594, geval = 0196
iter = 0196, obj = 2.30e-29, rnorm = 2.30e-29, gnorm = 4.15e-14, feval = 00597, geval = 0197
Stepper couldn't find a proper step size, will terminate solver
##########################################################################################
    Nonlinear CG Solver end
##########################################################################################

Let's plot the optimization path taken by the algorithm, which converged to the global minimum in 199 iterations using a parabolic stepper.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle(r"Nonlinear CG with FR beta function")
plt.show()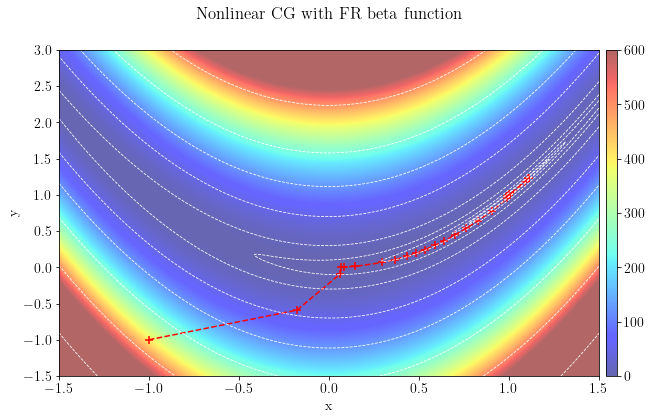

For the second test, we will test the steppest-descent approach using the same stepper.

NLSDsolver = o.NLCG(Stop, beta_type="SD")
Ros_prob = Rosenbrock(x_init, y_init)
NLSDsolver.setDefaults(save_obj=True, save_model=True)
NLSDsolver.run(Ros_prob, verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(NLSDsolver.model)):
    x_smpld.append(NLSDsolver.model[i][0])
    y_smpld.append(NLSDsolver.model[i][1])

##########################################################################################
            Nonlinear SD Solver 
    Restart folder: /tmp/restart_2022-04-22T01-49-07.409475/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 2.06e+01, rnorm = 2.06e+01, gnorm = 9.40e+01, feval = 00004, geval = 0002
iter = 0002, obj = 9.73e-01, rnorm = 9.73e-01, gnorm = 5.19e+00, feval = 00007, geval = 0003
iter = 0003, obj = 8.96e-01, rnorm = 8.96e-01, gnorm = 2.04e+00, feval = 00010, geval = 0004
iter = 0004, obj = 8.44e-01, rnorm = 8.44e-01, gnorm = 4.55e+00, feval = 00013, geval = 0005
iter = 0005, obj = 7.86e-01, rnorm = 7.86e-01, gnorm = 1.84e+00, feval = 00016, geval = 0006
iter = 0006, obj = 7.40e-01, rnorm = 7.40e-01, gnorm = 4.75e+00, feval = 00019, geval = 0007
iter = 0007, obj = 6.83e-01, rnorm = 6.83e-01, gnorm = 1.65e+00, feval = 00022, geval = 0008
iter = 0008, obj = 6.45e-01, rnorm = 6.45e-01, gnorm = 4.54e+00, feval = 00025, geval = 0009
iter = 0009, obj = 5.98e-01, rnorm = 5.98e-01, gnorm = 1.46e+00, feval = 00028, geval = 0010
iter = 0010, obj = 5.63e-01, rnorm = 5.63e-01, gnorm = 5.67e+00, feval = 00031, geval = 0011
iter = 0011, obj = 5.23e-01, rnorm = 5.23e-01, gnorm = 3.39e+00, feval = 00034, geval = 0012
iter = 0012, obj = 4.98e-01, rnorm = 4.98e-01, gnorm = 1.30e+00, feval = 00037, geval = 0013
iter = 0013, obj = 4.78e-01, rnorm = 4.78e-01, gnorm = 3.31e+00, feval = 00040, geval = 0014
iter = 0014, obj = 4.57e-01, rnorm = 4.57e-01, gnorm = 1.17e+00, feval = 00043, geval = 0015
iter = 0015, obj = 4.32e-01, rnorm = 4.32e-01, gnorm = 4.52e+00, feval = 00046, geval = 0016
iter = 0016, obj = 4.15e-01, rnorm = 4.15e-01, gnorm = 3.22e+00, feval = 00049, geval = 0017
iter = 0017, obj = 3.97e-01, rnorm = 3.97e-01, gnorm = 1.06e+00, feval = 00052, geval = 0018
iter = 0018, obj = 3.81e-01, rnorm = 3.81e-01, gnorm = 3.26e+00, feval = 00055, geval = 0019
iter = 0019, obj = 3.64e-01, rnorm = 3.64e-01, gnorm = 9.78e-01, feval = 00058, geval = 0020
iter = 0020, obj = 3.43e-01, rnorm = 3.43e-01, gnorm = 3.28e+00, feval = 00061, geval = 0021
iter = 0021, obj = 3.26e-01, rnorm = 3.26e-01, gnorm = 9.21e-01, feval = 00067, geval = 0022
iter = 0022, obj = 3.16e-01, rnorm = 3.16e-01, gnorm = 2.44e+00, feval = 00070, geval = 0023
iter = 0023, obj = 3.08e-01, rnorm = 3.08e-01, gnorm = 1.34e+00, feval = 00073, geval = 0024
iter = 0024, obj = 3.04e-01, rnorm = 3.04e-01, gnorm = 1.04e+00, feval = 00076, geval = 0025
iter = 0025, obj = 3.00e-01, rnorm = 3.00e-01, gnorm = 1.30e+00, feval = 00079, geval = 0026
iter = 0026, obj = 2.96e-01, rnorm = 2.96e-01, gnorm = 1.02e+00, feval = 00082, geval = 0027
iter = 0027, obj = 2.92e-01, rnorm = 2.92e-01, gnorm = 1.26e+00, feval = 00085, geval = 0028
iter = 0028, obj = 2.89e-01, rnorm = 2.89e-01, gnorm = 1.01e+00, feval = 00088, geval = 0029
iter = 0029, obj = 2.85e-01, rnorm = 2.85e-01, gnorm = 1.23e+00, feval = 00091, geval = 0030
iter = 0030, obj = 2.82e-01, rnorm = 2.82e-01, gnorm = 9.97e-01, feval = 00094, geval = 0031
iter = 0031, obj = 2.79e-01, rnorm = 2.79e-01, gnorm = 1.20e+00, feval = 00097, geval = 0032
iter = 0032, obj = 2.76e-01, rnorm = 2.76e-01, gnorm = 9.86e-01, feval = 00100, geval = 0033
iter = 0033, obj = 2.73e-01, rnorm = 2.73e-01, gnorm = 1.17e+00, feval = 00103, geval = 0034
iter = 0034, obj = 2.70e-01, rnorm = 2.70e-01, gnorm = 9.75e-01, feval = 00106, geval = 0035
iter = 0035, obj = 2.67e-01, rnorm = 2.67e-01, gnorm = 1.14e+00, feval = 00109, geval = 0036
iter = 0036, obj = 2.64e-01, rnorm = 2.64e-01, gnorm = 9.66e-01, feval = 00112, geval = 0037
iter = 0037, obj = 2.61e-01, rnorm = 2.61e-01, gnorm = 1.11e+00, feval = 00115, geval = 0038
iter = 0038, obj = 2.58e-01, rnorm = 2.58e-01, gnorm = 9.56e-01, feval = 00118, geval = 0039
iter = 0039, obj = 2.56e-01, rnorm = 2.56e-01, gnorm = 1.08e+00, feval = 00121, geval = 0040
iter = 0040, obj = 2.53e-01, rnorm = 2.53e-01, gnorm = 9.48e-01, feval = 00124, geval = 0041
iter = 0041, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 1.06e+00, feval = 00127, geval = 0042
iter = 0042, obj = 2.48e-01, rnorm = 2.48e-01, gnorm = 9.40e-01, feval = 00130, geval = 0043
iter = 0043, obj = 2.46e-01, rnorm = 2.46e-01, gnorm = 1.03e+00, feval = 00133, geval = 0044
iter = 0044, obj = 2.43e-01, rnorm = 2.43e-01, gnorm = 9.32e-01, feval = 00136, geval = 0045
iter = 0045, obj = 2.41e-01, rnorm = 2.41e-01, gnorm = 1.01e+00, feval = 00139, geval = 0046
iter = 0046, obj = 2.39e-01, rnorm = 2.39e-01, gnorm = 9.25e-01, feval = 00142, geval = 0047
iter = 0047, obj = 2.36e-01, rnorm = 2.36e-01, gnorm = 9.88e-01, feval = 00145, geval = 0048
iter = 0048, obj = 2.34e-01, rnorm = 2.34e-01, gnorm = 9.19e-01, feval = 00148, geval = 0049
iter = 0049, obj = 2.32e-01, rnorm = 2.32e-01, gnorm = 9.67e-01, feval = 00151, geval = 0050
iter = 0050, obj = 2.30e-01, rnorm = 2.30e-01, gnorm = 9.13e-01, feval = 00154, geval = 0051
iter = 0051, obj = 2.28e-01, rnorm = 2.28e-01, gnorm = 9.47e-01, feval = 00157, geval = 0052
iter = 0052, obj = 2.26e-01, rnorm = 2.26e-01, gnorm = 9.07e-01, feval = 00160, geval = 0053
iter = 0053, obj = 2.24e-01, rnorm = 2.24e-01, gnorm = 9.27e-01, feval = 00163, geval = 0054
iter = 0054, obj = 2.22e-01, rnorm = 2.22e-01, gnorm = 9.02e-01, feval = 00166, geval = 0055
iter = 0055, obj = 2.20e-01, rnorm = 2.20e-01, gnorm = 9.08e-01, feval = 00169, geval = 0056
iter = 0056, obj = 2.18e-01, rnorm = 2.18e-01, gnorm = 8.98e-01, feval = 00172, geval = 0057
iter = 0057, obj = 2.16e-01, rnorm = 2.16e-01, gnorm = 8.91e-01, feval = 00175, geval = 0058
iter = 0058, obj = 2.14e-01, rnorm = 2.14e-01, gnorm = 8.93e-01, feval = 00178, geval = 0059
iter = 0059, obj = 2.12e-01, rnorm = 2.12e-01, gnorm = 8.73e-01, feval = 00181, geval = 0060
iter = 0060, obj = 2.11e-01, rnorm = 2.11e-01, gnorm = 8.88e-01, feval = 00184, geval = 0061
iter = 0061, obj = 2.09e-01, rnorm = 2.09e-01, gnorm = 8.56e-01, feval = 00187, geval = 0062
iter = 0062, obj = 2.07e-01, rnorm = 2.07e-01, gnorm = 8.85e-01, feval = 00190, geval = 0063
iter = 0063, obj = 2.05e-01, rnorm = 2.05e-01, gnorm = 8.40e-01, feval = 00193, geval = 0064
iter = 0064, obj = 2.04e-01, rnorm = 2.04e-01, gnorm = 8.81e-01, feval = 00196, geval = 0065
iter = 0065, obj = 2.02e-01, rnorm = 2.02e-01, gnorm = 8.24e-01, feval = 00199, geval = 0066
iter = 0066, obj = 2.00e-01, rnorm = 2.00e-01, gnorm = 8.78e-01, feval = 00202, geval = 0067
iter = 0067, obj = 1.99e-01, rnorm = 1.99e-01, gnorm = 8.08e-01, feval = 00205, geval = 0068
iter = 0068, obj = 1.97e-01, rnorm = 1.97e-01, gnorm = 8.75e-01, feval = 00208, geval = 0069
iter = 0069, obj = 1.96e-01, rnorm = 1.96e-01, gnorm = 7.94e-01, feval = 00211, geval = 0070
iter = 0070, obj = 1.94e-01, rnorm = 1.94e-01, gnorm = 8.73e-01, feval = 00214, geval = 0071
iter = 0071, obj = 1.93e-01, rnorm = 1.93e-01, gnorm = 7.79e-01, feval = 00217, geval = 0072
iter = 0072, obj = 1.91e-01, rnorm = 1.91e-01, gnorm = 8.70e-01, feval = 00220, geval = 0073
iter = 0073, obj = 1.90e-01, rnorm = 1.90e-01, gnorm = 7.65e-01, feval = 00223, geval = 0074
iter = 0074, obj = 1.88e-01, rnorm = 1.88e-01, gnorm = 8.68e-01, feval = 00226, geval = 0075
iter = 0075, obj = 1.87e-01, rnorm = 1.87e-01, gnorm = 7.52e-01, feval = 00229, geval = 0076
iter = 0076, obj = 1.85e-01, rnorm = 1.85e-01, gnorm = 8.66e-01, feval = 00232, geval = 0077
iter = 0077, obj = 1.84e-01, rnorm = 1.84e-01, gnorm = 7.39e-01, feval = 00235, geval = 0078
iter = 0078, obj = 1.82e-01, rnorm = 1.82e-01, gnorm = 8.64e-01, feval = 00238, geval = 0079
iter = 0079, obj = 1.81e-01, rnorm = 1.81e-01, gnorm = 7.27e-01, feval = 00241, geval = 0080
iter = 0080, obj = 1.80e-01, rnorm = 1.80e-01, gnorm = 8.63e-01, feval = 00244, geval = 0081
iter = 0081, obj = 1.78e-01, rnorm = 1.78e-01, gnorm = 7.14e-01, feval = 00247, geval = 0082
iter = 0082, obj = 1.77e-01, rnorm = 1.77e-01, gnorm = 8.61e-01, feval = 00250, geval = 0083
iter = 0083, obj = 1.76e-01, rnorm = 1.76e-01, gnorm = 7.03e-01, feval = 00253, geval = 0084
iter = 0084, obj = 1.74e-01, rnorm = 1.74e-01, gnorm = 8.60e-01, feval = 00256, geval = 0085
iter = 0085, obj = 1.73e-01, rnorm = 1.73e-01, gnorm = 6.91e-01, feval = 00259, geval = 0086
iter = 0086, obj = 1.72e-01, rnorm = 1.72e-01, gnorm = 8.59e-01, feval = 00262, geval = 0087
iter = 0087, obj = 1.71e-01, rnorm = 1.71e-01, gnorm = 6.80e-01, feval = 00265, geval = 0088
iter = 0088, obj = 1.69e-01, rnorm = 1.69e-01, gnorm = 8.57e-01, feval = 00268, geval = 0089
iter = 0089, obj = 1.68e-01, rnorm = 1.68e-01, gnorm = 6.70e-01, feval = 00271, geval = 0090
iter = 0090, obj = 1.67e-01, rnorm = 1.67e-01, gnorm = 8.56e-01, feval = 00274, geval = 0091
iter = 0091, obj = 1.66e-01, rnorm = 1.66e-01, gnorm = 6.59e-01, feval = 00277, geval = 0092
iter = 0092, obj = 1.64e-01, rnorm = 1.64e-01, gnorm = 8.55e-01, feval = 00280, geval = 0093
iter = 0093, obj = 1.63e-01, rnorm = 1.63e-01, gnorm = 6.50e-01, feval = 00283, geval = 0094
iter = 0094, obj = 1.62e-01, rnorm = 1.62e-01, gnorm = 8.53e-01, feval = 00286, geval = 0095
iter = 0095, obj = 1.61e-01, rnorm = 1.61e-01, gnorm = 6.40e-01, feval = 00289, geval = 0096
iter = 0096, obj = 1.60e-01, rnorm = 1.60e-01, gnorm = 8.52e-01, feval = 00292, geval = 0097
iter = 0097, obj = 1.59e-01, rnorm = 1.59e-01, gnorm = 6.31e-01, feval = 00295, geval = 0098
iter = 0098, obj = 1.57e-01, rnorm = 1.57e-01, gnorm = 8.50e-01, feval = 00298, geval = 0099
iter = 0099, obj = 1.56e-01, rnorm = 1.56e-01, gnorm = 6.22e-01, feval = 00301, geval = 0100
iter = 0100, obj = 1.55e-01, rnorm = 1.55e-01, gnorm = 8.49e-01, feval = 00304, geval = 0101
iter = 0101, obj = 1.54e-01, rnorm = 1.54e-01, gnorm = 6.13e-01, feval = 00307, geval = 0102
iter = 0102, obj = 1.53e-01, rnorm = 1.53e-01, gnorm = 8.47e-01, feval = 00310, geval = 0103
iter = 0103, obj = 1.52e-01, rnorm = 1.52e-01, gnorm = 6.05e-01, feval = 00313, geval = 0104
iter = 0104, obj = 1.51e-01, rnorm = 1.51e-01, gnorm = 8.45e-01, feval = 00316, geval = 0105
iter = 0105, obj = 1.50e-01, rnorm = 1.50e-01, gnorm = 5.97e-01, feval = 00319, geval = 0106
iter = 0106, obj = 1.49e-01, rnorm = 1.49e-01, gnorm = 8.42e-01, feval = 00322, geval = 0107
iter = 0107, obj = 1.48e-01, rnorm = 1.48e-01, gnorm = 5.89e-01, feval = 00325, geval = 0108
iter = 0108, obj = 1.47e-01, rnorm = 1.47e-01, gnorm = 8.40e-01, feval = 00328, geval = 0109
iter = 0109, obj = 1.45e-01, rnorm = 1.45e-01, gnorm = 5.82e-01, feval = 00331, geval = 0110
iter = 0110, obj = 1.44e-01, rnorm = 1.44e-01, gnorm = 8.37e-01, feval = 00334, geval = 0111
iter = 0111, obj = 1.43e-01, rnorm = 1.43e-01, gnorm = 5.74e-01, feval = 00337, geval = 0112
iter = 0112, obj = 1.42e-01, rnorm = 1.42e-01, gnorm = 8.34e-01, feval = 00340, geval = 0113
iter = 0113, obj = 1.41e-01, rnorm = 1.41e-01, gnorm = 5.67e-01, feval = 00343, geval = 0114
iter = 0114, obj = 1.40e-01, rnorm = 1.40e-01, gnorm = 8.31e-01, feval = 00346, geval = 0115
iter = 0115, obj = 1.39e-01, rnorm = 1.39e-01, gnorm = 5.61e-01, feval = 00349, geval = 0116
iter = 0116, obj = 1.39e-01, rnorm = 1.39e-01, gnorm = 8.27e-01, feval = 00352, geval = 0117
iter = 0117, obj = 1.38e-01, rnorm = 1.38e-01, gnorm = 5.54e-01, feval = 00355, geval = 0118
iter = 0118, obj = 1.37e-01, rnorm = 1.37e-01, gnorm = 8.23e-01, feval = 00358, geval = 0119
iter = 0119, obj = 1.36e-01, rnorm = 1.36e-01, gnorm = 5.48e-01, feval = 00361, geval = 0120
iter = 0120, obj = 1.35e-01, rnorm = 1.35e-01, gnorm = 8.19e-01, feval = 00364, geval = 0121
iter = 0121, obj = 1.34e-01, rnorm = 1.34e-01, gnorm = 5.42e-01, feval = 00367, geval = 0122
iter = 0122, obj = 1.33e-01, rnorm = 1.33e-01, gnorm = 8.15e-01, feval = 00370, geval = 0123
iter = 0123, obj = 1.32e-01, rnorm = 1.32e-01, gnorm = 5.36e-01, feval = 00373, geval = 0124
iter = 0124, obj = 1.31e-01, rnorm = 1.31e-01, gnorm = 8.10e-01, feval = 00376, geval = 0125
iter = 0125, obj = 1.30e-01, rnorm = 1.30e-01, gnorm = 5.30e-01, feval = 00379, geval = 0126
iter = 0126, obj = 1.29e-01, rnorm = 1.29e-01, gnorm = 8.06e-01, feval = 00382, geval = 0127
iter = 0127, obj = 1.28e-01, rnorm = 1.28e-01, gnorm = 5.25e-01, feval = 00385, geval = 0128
iter = 0128, obj = 1.28e-01, rnorm = 1.28e-01, gnorm = 8.01e-01, feval = 00388, geval = 0129
iter = 0129, obj = 1.27e-01, rnorm = 1.27e-01, gnorm = 5.19e-01, feval = 00391, geval = 0130
iter = 0130, obj = 1.26e-01, rnorm = 1.26e-01, gnorm = 7.96e-01, feval = 00394, geval = 0131
iter = 0131, obj = 1.25e-01, rnorm = 1.25e-01, gnorm = 5.14e-01, feval = 00397, geval = 0132
iter = 0132, obj = 1.24e-01, rnorm = 1.24e-01, gnorm = 7.91e-01, feval = 00400, geval = 0133
iter = 0133, obj = 1.23e-01, rnorm = 1.23e-01, gnorm = 5.09e-01, feval = 00403, geval = 0134
iter = 0134, obj = 1.23e-01, rnorm = 1.23e-01, gnorm = 7.86e-01, feval = 00406, geval = 0135
iter = 0135, obj = 1.22e-01, rnorm = 1.22e-01, gnorm = 5.04e-01, feval = 00409, geval = 0136
iter = 0136, obj = 1.21e-01, rnorm = 1.21e-01, gnorm = 7.80e-01, feval = 00412, geval = 0137
iter = 0137, obj = 1.20e-01, rnorm = 1.20e-01, gnorm = 4.99e-01, feval = 00415, geval = 0138
iter = 0138, obj = 1.19e-01, rnorm = 1.19e-01, gnorm = 7.75e-01, feval = 00418, geval = 0139
iter = 0139, obj = 1.19e-01, rnorm = 1.19e-01, gnorm = 4.95e-01, feval = 00421, geval = 0140
iter = 0140, obj = 1.18e-01, rnorm = 1.18e-01, gnorm = 7.70e-01, feval = 00424, geval = 0141
iter = 0141, obj = 1.17e-01, rnorm = 1.17e-01, gnorm = 4.90e-01, feval = 00427, geval = 0142
iter = 0142, obj = 1.16e-01, rnorm = 1.16e-01, gnorm = 7.64e-01, feval = 00430, geval = 0143
iter = 0143, obj = 1.16e-01, rnorm = 1.16e-01, gnorm = 4.86e-01, feval = 00433, geval = 0144
iter = 0144, obj = 1.15e-01, rnorm = 1.15e-01, gnorm = 7.59e-01, feval = 00436, geval = 0145
iter = 0145, obj = 1.14e-01, rnorm = 1.14e-01, gnorm = 4.81e-01, feval = 00439, geval = 0146
iter = 0146, obj = 1.13e-01, rnorm = 1.13e-01, gnorm = 7.53e-01, feval = 00442, geval = 0147
iter = 0147, obj = 1.13e-01, rnorm = 1.13e-01, gnorm = 4.77e-01, feval = 00445, geval = 0148
iter = 0148, obj = 1.12e-01, rnorm = 1.12e-01, gnorm = 7.48e-01, feval = 00448, geval = 0149
iter = 0149, obj = 1.11e-01, rnorm = 1.11e-01, gnorm = 4.73e-01, feval = 00451, geval = 0150
iter = 0150, obj = 1.11e-01, rnorm = 1.11e-01, gnorm = 7.42e-01, feval = 00454, geval = 0151
iter = 0151, obj = 1.10e-01, rnorm = 1.10e-01, gnorm = 4.69e-01, feval = 00457, geval = 0152
iter = 0152, obj = 1.09e-01, rnorm = 1.09e-01, gnorm = 7.37e-01, feval = 00460, geval = 0153
iter = 0153, obj = 1.08e-01, rnorm = 1.08e-01, gnorm = 4.65e-01, feval = 00463, geval = 0154
iter = 0154, obj = 1.08e-01, rnorm = 1.08e-01, gnorm = 7.31e-01, feval = 00466, geval = 0155
iter = 0155, obj = 1.07e-01, rnorm = 1.07e-01, gnorm = 4.61e-01, feval = 00469, geval = 0156
iter = 0156, obj = 1.06e-01, rnorm = 1.06e-01, gnorm = 7.26e-01, feval = 00472, geval = 0157
iter = 0157, obj = 1.06e-01, rnorm = 1.06e-01, gnorm = 4.57e-01, feval = 00475, geval = 0158
iter = 0158, obj = 1.05e-01, rnorm = 1.05e-01, gnorm = 7.21e-01, feval = 00478, geval = 0159
iter = 0159, obj = 1.05e-01, rnorm = 1.05e-01, gnorm = 4.54e-01, feval = 00481, geval = 0160
iter = 0160, obj = 1.04e-01, rnorm = 1.04e-01, gnorm = 7.15e-01, feval = 00484, geval = 0161
iter = 0161, obj = 1.03e-01, rnorm = 1.03e-01, gnorm = 4.50e-01, feval = 00487, geval = 0162
iter = 0162, obj = 1.03e-01, rnorm = 1.03e-01, gnorm = 7.10e-01, feval = 00490, geval = 0163
iter = 0163, obj = 1.02e-01, rnorm = 1.02e-01, gnorm = 4.46e-01, feval = 00493, geval = 0164
iter = 0164, obj = 1.01e-01, rnorm = 1.01e-01, gnorm = 7.05e-01, feval = 00496, geval = 0165
iter = 0165, obj = 1.01e-01, rnorm = 1.01e-01, gnorm = 4.43e-01, feval = 00499, geval = 0166
iter = 0166, obj = 1.00e-01, rnorm = 1.00e-01, gnorm = 7.00e-01, feval = 00502, geval = 0167
iter = 0167, obj = 9.97e-02, rnorm = 9.97e-02, gnorm = 4.39e-01, feval = 00505, geval = 0168
iter = 0168, obj = 9.91e-02, rnorm = 9.91e-02, gnorm = 6.94e-01, feval = 00508, geval = 0169
iter = 0169, obj = 9.85e-02, rnorm = 9.85e-02, gnorm = 4.36e-01, feval = 00511, geval = 0170
iter = 0170, obj = 9.79e-02, rnorm = 9.79e-02, gnorm = 6.89e-01, feval = 00514, geval = 0171
iter = 0171, obj = 9.73e-02, rnorm = 9.73e-02, gnorm = 4.33e-01, feval = 00517, geval = 0172
iter = 0172, obj = 9.68e-02, rnorm = 9.68e-02, gnorm = 6.84e-01, feval = 00520, geval = 0173
iter = 0173, obj = 9.62e-02, rnorm = 9.62e-02, gnorm = 4.29e-01, feval = 00523, geval = 0174
iter = 0174, obj = 9.57e-02, rnorm = 9.57e-02, gnorm = 6.79e-01, feval = 00526, geval = 0175
iter = 0175, obj = 9.51e-02, rnorm = 9.51e-02, gnorm = 4.26e-01, feval = 00529, geval = 0176
iter = 0176, obj = 9.46e-02, rnorm = 9.46e-02, gnorm = 6.74e-01, feval = 00532, geval = 0177
iter = 0177, obj = 9.40e-02, rnorm = 9.40e-02, gnorm = 4.23e-01, feval = 00535, geval = 0178
iter = 0178, obj = 9.35e-02, rnorm = 9.35e-02, gnorm = 6.70e-01, feval = 00538, geval = 0179
iter = 0179, obj = 9.30e-02, rnorm = 9.30e-02, gnorm = 4.20e-01, feval = 00541, geval = 0180
iter = 0180, obj = 9.24e-02, rnorm = 9.24e-02, gnorm = 6.65e-01, feval = 00544, geval = 0181
iter = 0181, obj = 9.19e-02, rnorm = 9.19e-02, gnorm = 4.17e-01, feval = 00547, geval = 0182
iter = 0182, obj = 9.14e-02, rnorm = 9.14e-02, gnorm = 6.60e-01, feval = 00550, geval = 0183
iter = 0183, obj = 9.09e-02, rnorm = 9.09e-02, gnorm = 4.14e-01, feval = 00553, geval = 0184
iter = 0184, obj = 9.04e-02, rnorm = 9.04e-02, gnorm = 6.55e-01, feval = 00556, geval = 0185
iter = 0185, obj = 8.99e-02, rnorm = 8.99e-02, gnorm = 4.11e-01, feval = 00559, geval = 0186
iter = 0186, obj = 8.94e-02, rnorm = 8.94e-02, gnorm = 6.51e-01, feval = 00562, geval = 0187
iter = 0187, obj = 8.89e-02, rnorm = 8.89e-02, gnorm = 4.08e-01, feval = 00565, geval = 0188
iter = 0188, obj = 8.84e-02, rnorm = 8.84e-02, gnorm = 6.46e-01, feval = 00568, geval = 0189
iter = 0189, obj = 8.79e-02, rnorm = 8.79e-02, gnorm = 4.05e-01, feval = 00571, geval = 0190
iter = 0190, obj = 8.74e-02, rnorm = 8.74e-02, gnorm = 6.42e-01, feval = 00574, geval = 0191
iter = 0191, obj = 8.69e-02, rnorm = 8.69e-02, gnorm = 4.02e-01, feval = 00577, geval = 0192
iter = 0192, obj = 8.65e-02, rnorm = 8.65e-02, gnorm = 6.37e-01, feval = 00580, geval = 0193
iter = 0193, obj = 8.60e-02, rnorm = 8.60e-02, gnorm = 3.99e-01, feval = 00583, geval = 0194
iter = 0194, obj = 8.55e-02, rnorm = 8.55e-02, gnorm = 6.33e-01, feval = 00586, geval = 0195
iter = 0195, obj = 8.51e-02, rnorm = 8.51e-02, gnorm = 3.96e-01, feval = 00589, geval = 0196
iter = 0196, obj = 8.46e-02, rnorm = 8.46e-02, gnorm = 6.29e-01, feval = 00592, geval = 0197
iter = 0197, obj = 8.41e-02, rnorm = 8.41e-02, gnorm = 3.94e-01, feval = 00595, geval = 0198
iter = 0198, obj = 8.37e-02, rnorm = 8.37e-02, gnorm = 6.24e-01, feval = 00598, geval = 0199
iter = 0199, obj = 8.32e-02, rnorm = 8.32e-02, gnorm = 3.91e-01, feval = 00601, geval = 0200
iter = 0200, obj = 8.28e-02, rnorm = 8.28e-02, gnorm = 6.20e-01, feval = 00604, geval = 0201
iter = 0201, obj = 8.24e-02, rnorm = 8.24e-02, gnorm = 3.88e-01, feval = 00607, geval = 0202
iter = 0202, obj = 8.19e-02, rnorm = 8.19e-02, gnorm = 6.16e-01, feval = 00610, geval = 0203
iter = 0203, obj = 8.15e-02, rnorm = 8.15e-02, gnorm = 3.86e-01, feval = 00613, geval = 0204
iter = 0204, obj = 8.11e-02, rnorm = 8.11e-02, gnorm = 6.12e-01, feval = 00616, geval = 0205
iter = 0205, obj = 8.06e-02, rnorm = 8.06e-02, gnorm = 3.83e-01, feval = 00619, geval = 0206
iter = 0206, obj = 8.02e-02, rnorm = 8.02e-02, gnorm = 6.08e-01, feval = 00622, geval = 0207
iter = 0207, obj = 7.98e-02, rnorm = 7.98e-02, gnorm = 3.81e-01, feval = 00625, geval = 0208
iter = 0208, obj = 7.94e-02, rnorm = 7.94e-02, gnorm = 6.04e-01, feval = 00628, geval = 0209
iter = 0209, obj = 7.90e-02, rnorm = 7.90e-02, gnorm = 3.78e-01, feval = 00631, geval = 0210
iter = 0210, obj = 7.85e-02, rnorm = 7.85e-02, gnorm = 6.00e-01, feval = 00634, geval = 0211
iter = 0211, obj = 7.81e-02, rnorm = 7.81e-02, gnorm = 3.76e-01, feval = 00637, geval = 0212
iter = 0212, obj = 7.77e-02, rnorm = 7.77e-02, gnorm = 5.96e-01, feval = 00640, geval = 0213
iter = 0213, obj = 7.73e-02, rnorm = 7.73e-02, gnorm = 3.73e-01, feval = 00643, geval = 0214
iter = 0214, obj = 7.69e-02, rnorm = 7.69e-02, gnorm = 5.92e-01, feval = 00646, geval = 0215
iter = 0215, obj = 7.65e-02, rnorm = 7.65e-02, gnorm = 3.71e-01, feval = 00649, geval = 0216
iter = 0216, obj = 7.62e-02, rnorm = 7.62e-02, gnorm = 5.88e-01, feval = 00652, geval = 0217
iter = 0217, obj = 7.58e-02, rnorm = 7.58e-02, gnorm = 3.68e-01, feval = 00655, geval = 0218

iter = 0218, obj = 7.54e-02, rnorm = 7.54e-02, gnorm = 5.85e-01, feval = 00658, geval = 0219
iter = 0219, obj = 7.50e-02, rnorm = 7.50e-02, gnorm = 3.66e-01, feval = 00661, geval = 0220
iter = 0220, obj = 7.46e-02, rnorm = 7.46e-02, gnorm = 5.81e-01, feval = 00664, geval = 0221
iter = 0221, obj = 7.42e-02, rnorm = 7.42e-02, gnorm = 3.64e-01, feval = 00667, geval = 0222
iter = 0222, obj = 7.39e-02, rnorm = 7.39e-02, gnorm = 5.77e-01, feval = 00670, geval = 0223
iter = 0223, obj = 7.35e-02, rnorm = 7.35e-02, gnorm = 3.62e-01, feval = 00673, geval = 0224
iter = 0224, obj = 7.31e-02, rnorm = 7.31e-02, gnorm = 5.73e-01, feval = 00676, geval = 0225
iter = 0225, obj = 7.28e-02, rnorm = 7.28e-02, gnorm = 3.59e-01, feval = 00679, geval = 0226
iter = 0226, obj = 7.24e-02, rnorm = 7.24e-02, gnorm = 5.70e-01, feval = 00682, geval = 0227
iter = 0227, obj = 7.20e-02, rnorm = 7.20e-02, gnorm = 3.57e-01, feval = 00685, geval = 0228
iter = 0228, obj = 7.17e-02, rnorm = 7.17e-02, gnorm = 5.66e-01, feval = 00688, geval = 0229
iter = 0229, obj = 7.13e-02, rnorm = 7.13e-02, gnorm = 3.55e-01, feval = 00691, geval = 0230
iter = 0230, obj = 7.10e-02, rnorm = 7.10e-02, gnorm = 5.63e-01, feval = 00694, geval = 0231
iter = 0231, obj = 7.06e-02, rnorm = 7.06e-02, gnorm = 3.53e-01, feval = 00697, geval = 0232
iter = 0232, obj = 7.03e-02, rnorm = 7.03e-02, gnorm = 5.59e-01, feval = 00700, geval = 0233
iter = 0233, obj = 6.99e-02, rnorm = 6.99e-02, gnorm = 3.51e-01, feval = 00703, geval = 0234
iter = 0234, obj = 6.96e-02, rnorm = 6.96e-02, gnorm = 5.56e-01, feval = 00706, geval = 0235
iter = 0235, obj = 6.93e-02, rnorm = 6.93e-02, gnorm = 3.48e-01, feval = 00709, geval = 0236
iter = 0236, obj = 6.89e-02, rnorm = 6.89e-02, gnorm = 5.53e-01, feval = 00712, geval = 0237
iter = 0237, obj = 6.86e-02, rnorm = 6.86e-02, gnorm = 3.46e-01, feval = 00715, geval = 0238
iter = 0238, obj = 6.83e-02, rnorm = 6.83e-02, gnorm = 5.49e-01, feval = 00718, geval = 0239
iter = 0239, obj = 6.79e-02, rnorm = 6.79e-02, gnorm = 3.44e-01, feval = 00721, geval = 0240
iter = 0240, obj = 6.76e-02, rnorm = 6.76e-02, gnorm = 5.46e-01, feval = 00724, geval = 0241
iter = 0241, obj = 6.73e-02, rnorm = 6.73e-02, gnorm = 3.42e-01, feval = 00727, geval = 0242
iter = 0242, obj = 6.70e-02, rnorm = 6.70e-02, gnorm = 5.43e-01, feval = 00730, geval = 0243
iter = 0243, obj = 6.66e-02, rnorm = 6.66e-02, gnorm = 3.40e-01, feval = 00733, geval = 0244
iter = 0244, obj = 6.63e-02, rnorm = 6.63e-02, gnorm = 5.40e-01, feval = 00736, geval = 0245
iter = 0245, obj = 6.60e-02, rnorm = 6.60e-02, gnorm = 3.38e-01, feval = 00739, geval = 0246
iter = 0246, obj = 6.57e-02, rnorm = 6.57e-02, gnorm = 5.36e-01, feval = 00742, geval = 0247
iter = 0247, obj = 6.54e-02, rnorm = 6.54e-02, gnorm = 3.36e-01, feval = 00745, geval = 0248
iter = 0248, obj = 6.51e-02, rnorm = 6.51e-02, gnorm = 5.33e-01, feval = 00748, geval = 0249
iter = 0249, obj = 6.48e-02, rnorm = 6.48e-02, gnorm = 3.34e-01, feval = 00751, geval = 0250
iter = 0250, obj = 6.45e-02, rnorm = 6.45e-02, gnorm = 5.30e-01, feval = 00754, geval = 0251
iter = 0251, obj = 6.42e-02, rnorm = 6.42e-02, gnorm = 3.32e-01, feval = 00757, geval = 0252
iter = 0252, obj = 6.39e-02, rnorm = 6.39e-02, gnorm = 5.27e-01, feval = 00760, geval = 0253
iter = 0253, obj = 6.36e-02, rnorm = 6.36e-02, gnorm = 3.30e-01, feval = 00763, geval = 0254
iter = 0254, obj = 6.33e-02, rnorm = 6.33e-02, gnorm = 5.24e-01, feval = 00766, geval = 0255
iter = 0255, obj = 6.30e-02, rnorm = 6.30e-02, gnorm = 3.29e-01, feval = 00769, geval = 0256
iter = 0256, obj = 6.27e-02, rnorm = 6.27e-02, gnorm = 5.21e-01, feval = 00772, geval = 0257
iter = 0257, obj = 6.24e-02, rnorm = 6.24e-02, gnorm = 3.27e-01, feval = 00775, geval = 0258
iter = 0258, obj = 6.21e-02, rnorm = 6.21e-02, gnorm = 5.18e-01, feval = 00778, geval = 0259
iter = 0259, obj = 6.18e-02, rnorm = 6.18e-02, gnorm = 3.25e-01, feval = 00781, geval = 0260
iter = 0260, obj = 6.15e-02, rnorm = 6.15e-02, gnorm = 5.15e-01, feval = 00784, geval = 0261
iter = 0261, obj = 6.13e-02, rnorm = 6.13e-02, gnorm = 3.23e-01, feval = 00787, geval = 0262
iter = 0262, obj = 6.10e-02, rnorm = 6.10e-02, gnorm = 5.12e-01, feval = 00790, geval = 0263
iter = 0263, obj = 6.07e-02, rnorm = 6.07e-02, gnorm = 3.21e-01, feval = 00793, geval = 0264
iter = 0264, obj = 6.04e-02, rnorm = 6.04e-02, gnorm = 5.09e-01, feval = 00796, geval = 0265
iter = 0265, obj = 6.01e-02, rnorm = 6.01e-02, gnorm = 3.19e-01, feval = 00799, geval = 0266
iter = 0266, obj = 5.99e-02, rnorm = 5.99e-02, gnorm = 5.06e-01, feval = 00802, geval = 0267
iter = 0267, obj = 5.96e-02, rnorm = 5.96e-02, gnorm = 3.18e-01, feval = 00805, geval = 0268
iter = 0268, obj = 5.93e-02, rnorm = 5.93e-02, gnorm = 5.04e-01, feval = 00808, geval = 0269
iter = 0269, obj = 5.91e-02, rnorm = 5.91e-02, gnorm = 3.16e-01, feval = 00811, geval = 0270
iter = 0270, obj = 5.88e-02, rnorm = 5.88e-02, gnorm = 5.01e-01, feval = 00814, geval = 0271
iter = 0271, obj = 5.85e-02, rnorm = 5.85e-02, gnorm = 3.14e-01, feval = 00817, geval = 0272
iter = 0272, obj = 5.83e-02, rnorm = 5.83e-02, gnorm = 4.98e-01, feval = 00820, geval = 0273
iter = 0273, obj = 5.80e-02, rnorm = 5.80e-02, gnorm = 3.12e-01, feval = 00823, geval = 0274
iter = 0274, obj = 5.77e-02, rnorm = 5.77e-02, gnorm = 4.95e-01, feval = 00826, geval = 0275
iter = 0275, obj = 5.75e-02, rnorm = 5.75e-02, gnorm = 3.11e-01, feval = 00829, geval = 0276
iter = 0276, obj = 5.72e-02, rnorm = 5.72e-02, gnorm = 4.93e-01, feval = 00832, geval = 0277
iter = 0277, obj = 5.70e-02, rnorm = 5.70e-02, gnorm = 3.09e-01, feval = 00835, geval = 0278
iter = 0278, obj = 5.67e-02, rnorm = 5.67e-02, gnorm = 4.90e-01, feval = 00838, geval = 0279
iter = 0279, obj = 5.65e-02, rnorm = 5.65e-02, gnorm = 3.07e-01, feval = 00841, geval = 0280
iter = 0280, obj = 5.62e-02, rnorm = 5.62e-02, gnorm = 4.87e-01, feval = 00844, geval = 0281
iter = 0281, obj = 5.60e-02, rnorm = 5.60e-02, gnorm = 3.06e-01, feval = 00847, geval = 0282
iter = 0282, obj = 5.57e-02, rnorm = 5.57e-02, gnorm = 4.85e-01, feval = 00850, geval = 0283
iter = 0283, obj = 5.55e-02, rnorm = 5.55e-02, gnorm = 3.04e-01, feval = 00853, geval = 0284
iter = 0284, obj = 5.52e-02, rnorm = 5.52e-02, gnorm = 4.82e-01, feval = 00856, geval = 0285
iter = 0285, obj = 5.50e-02, rnorm = 5.50e-02, gnorm = 3.03e-01, feval = 00859, geval = 0286
iter = 0286, obj = 5.48e-02, rnorm = 5.48e-02, gnorm = 4.79e-01, feval = 00862, geval = 0287
iter = 0287, obj = 5.45e-02, rnorm = 5.45e-02, gnorm = 3.01e-01, feval = 00865, geval = 0288
iter = 0288, obj = 5.43e-02, rnorm = 5.43e-02, gnorm = 4.77e-01, feval = 00868, geval = 0289
iter = 0289, obj = 5.40e-02, rnorm = 5.40e-02, gnorm = 2.99e-01, feval = 00871, geval = 0290
iter = 0290, obj = 5.38e-02, rnorm = 5.38e-02, gnorm = 4.74e-01, feval = 00874, geval = 0291
iter = 0291, obj = 5.36e-02, rnorm = 5.36e-02, gnorm = 2.98e-01, feval = 00877, geval = 0292
iter = 0292, obj = 5.33e-02, rnorm = 5.33e-02, gnorm = 4.72e-01, feval = 00880, geval = 0293
iter = 0293, obj = 5.31e-02, rnorm = 5.31e-02, gnorm = 2.96e-01, feval = 00883, geval = 0294
iter = 0294, obj = 5.29e-02, rnorm = 5.29e-02, gnorm = 4.69e-01, feval = 00886, geval = 0295
iter = 0295, obj = 5.27e-02, rnorm = 5.27e-02, gnorm = 2.95e-01, feval = 00889, geval = 0296
iter = 0296, obj = 5.24e-02, rnorm = 5.24e-02, gnorm = 4.67e-01, feval = 00892, geval = 0297
iter = 0297, obj = 5.22e-02, rnorm = 5.22e-02, gnorm = 2.93e-01, feval = 00895, geval = 0298
iter = 0298, obj = 5.20e-02, rnorm = 5.20e-02, gnorm = 4.65e-01, feval = 00898, geval = 0299
iter = 0299, obj = 5.18e-02, rnorm = 5.18e-02, gnorm = 2.92e-01, feval = 00901, geval = 0300
iter = 0300, obj = 5.15e-02, rnorm = 5.15e-02, gnorm = 4.62e-01, feval = 00904, geval = 0301
iter = 0301, obj = 5.13e-02, rnorm = 5.13e-02, gnorm = 2.90e-01, feval = 00907, geval = 0302
iter = 0302, obj = 5.11e-02, rnorm = 5.11e-02, gnorm = 4.60e-01, feval = 00910, geval = 0303
iter = 0303, obj = 5.09e-02, rnorm = 5.09e-02, gnorm = 2.89e-01, feval = 00913, geval = 0304
iter = 0304, obj = 5.07e-02, rnorm = 5.07e-02, gnorm = 4.57e-01, feval = 00916, geval = 0305
iter = 0305, obj = 5.05e-02, rnorm = 5.05e-02, gnorm = 2.87e-01, feval = 00919, geval = 0306
iter = 0306, obj = 5.03e-02, rnorm = 5.03e-02, gnorm = 4.55e-01, feval = 00922, geval = 0307
iter = 0307, obj = 5.00e-02, rnorm = 5.00e-02, gnorm = 2.86e-01, feval = 00925, geval = 0308
iter = 0308, obj = 4.98e-02, rnorm = 4.98e-02, gnorm = 4.53e-01, feval = 00928, geval = 0309
iter = 0309, obj = 4.96e-02, rnorm = 4.96e-02, gnorm = 2.84e-01, feval = 00931, geval = 0310
iter = 0310, obj = 4.94e-02, rnorm = 4.94e-02, gnorm = 4.50e-01, feval = 00934, geval = 0311
iter = 0311, obj = 4.92e-02, rnorm = 4.92e-02, gnorm = 2.83e-01, feval = 00937, geval = 0312
iter = 0312, obj = 4.90e-02, rnorm = 4.90e-02, gnorm = 4.48e-01, feval = 00940, geval = 0313
iter = 0313, obj = 4.88e-02, rnorm = 4.88e-02, gnorm = 2.82e-01, feval = 00943, geval = 0314
iter = 0314, obj = 4.86e-02, rnorm = 4.86e-02, gnorm = 4.46e-01, feval = 00946, geval = 0315
iter = 0315, obj = 4.84e-02, rnorm = 4.84e-02, gnorm = 2.80e-01, feval = 00949, geval = 0316
iter = 0316, obj = 4.82e-02, rnorm = 4.82e-02, gnorm = 4.44e-01, feval = 00952, geval = 0317
iter = 0317, obj = 4.80e-02, rnorm = 4.80e-02, gnorm = 2.79e-01, feval = 00955, geval = 0318
iter = 0318, obj = 4.78e-02, rnorm = 4.78e-02, gnorm = 4.42e-01, feval = 00958, geval = 0319
iter = 0319, obj = 4.76e-02, rnorm = 4.76e-02, gnorm = 2.77e-01, feval = 00961, geval = 0320
iter = 0320, obj = 4.74e-02, rnorm = 4.74e-02, gnorm = 4.39e-01, feval = 00964, geval = 0321
iter = 0321, obj = 4.72e-02, rnorm = 4.72e-02, gnorm = 2.76e-01, feval = 00967, geval = 0322
iter = 0322, obj = 4.70e-02, rnorm = 4.70e-02, gnorm = 4.37e-01, feval = 00970, geval = 0323
iter = 0323, obj = 4.68e-02, rnorm = 4.68e-02, gnorm = 2.75e-01, feval = 00973, geval = 0324
iter = 0324, obj = 4.66e-02, rnorm = 4.66e-02, gnorm = 4.35e-01, feval = 00976, geval = 0325
iter = 0325, obj = 4.64e-02, rnorm = 4.64e-02, gnorm = 2.73e-01, feval = 00979, geval = 0326
iter = 0326, obj = 4.63e-02, rnorm = 4.63e-02, gnorm = 4.33e-01, feval = 00982, geval = 0327
iter = 0327, obj = 4.61e-02, rnorm = 4.61e-02, gnorm = 2.72e-01, feval = 00985, geval = 0328
iter = 0328, obj = 4.59e-02, rnorm = 4.59e-02, gnorm = 4.31e-01, feval = 00988, geval = 0329
iter = 0329, obj = 4.57e-02, rnorm = 4.57e-02, gnorm = 2.71e-01, feval = 00991, geval = 0330
iter = 0330, obj = 4.55e-02, rnorm = 4.55e-02, gnorm = 4.29e-01, feval = 00994, geval = 0331
iter = 0331, obj = 4.53e-02, rnorm = 4.53e-02, gnorm = 2.69e-01, feval = 00997, geval = 0332
iter = 0332, obj = 4.51e-02, rnorm = 4.51e-02, gnorm = 4.27e-01, feval = 01000, geval = 0333
iter = 0333, obj = 4.50e-02, rnorm = 4.50e-02, gnorm = 2.68e-01, feval = 01003, geval = 0334
iter = 0334, obj = 4.48e-02, rnorm = 4.48e-02, gnorm = 4.25e-01, feval = 01006, geval = 0335
iter = 0335, obj = 4.46e-02, rnorm = 4.46e-02, gnorm = 2.67e-01, feval = 01009, geval = 0336
iter = 0336, obj = 4.44e-02, rnorm = 4.44e-02, gnorm = 4.23e-01, feval = 01012, geval = 0337
iter = 0337, obj = 4.42e-02, rnorm = 4.42e-02, gnorm = 2.66e-01, feval = 01015, geval = 0338
iter = 0338, obj = 4.41e-02, rnorm = 4.41e-02, gnorm = 4.21e-01, feval = 01018, geval = 0339
iter = 0339, obj = 4.39e-02, rnorm = 4.39e-02, gnorm = 2.64e-01, feval = 01021, geval = 0340
iter = 0340, obj = 4.37e-02, rnorm = 4.37e-02, gnorm = 4.19e-01, feval = 01024, geval = 0341
iter = 0341, obj = 4.35e-02, rnorm = 4.35e-02, gnorm = 2.63e-01, feval = 01027, geval = 0342
iter = 0342, obj = 4.34e-02, rnorm = 4.34e-02, gnorm = 4.17e-01, feval = 01030, geval = 0343
iter = 0343, obj = 4.32e-02, rnorm = 4.32e-02, gnorm = 2.62e-01, feval = 01033, geval = 0344
iter = 0344, obj = 4.30e-02, rnorm = 4.30e-02, gnorm = 4.15e-01, feval = 01036, geval = 0345
iter = 0345, obj = 4.29e-02, rnorm = 4.29e-02, gnorm = 2.61e-01, feval = 01039, geval = 0346
iter = 0346, obj = 4.27e-02, rnorm = 4.27e-02, gnorm = 4.13e-01, feval = 01042, geval = 0347
iter = 0347, obj = 4.25e-02, rnorm = 4.25e-02, gnorm = 2.59e-01, feval = 01045, geval = 0348
iter = 0348, obj = 4.23e-02, rnorm = 4.23e-02, gnorm = 4.11e-01, feval = 01048, geval = 0349
iter = 0349, obj = 4.22e-02, rnorm = 4.22e-02, gnorm = 2.58e-01, feval = 01051, geval = 0350
iter = 0350, obj = 4.20e-02, rnorm = 4.20e-02, gnorm = 4.09e-01, feval = 01054, geval = 0351
iter = 0351, obj = 4.19e-02, rnorm = 4.19e-02, gnorm = 2.57e-01, feval = 01057, geval = 0352
iter = 0352, obj = 4.17e-02, rnorm = 4.17e-02, gnorm = 4.07e-01, feval = 01060, geval = 0353
iter = 0353, obj = 4.15e-02, rnorm = 4.15e-02, gnorm = 2.56e-01, feval = 01063, geval = 0354
iter = 0354, obj = 4.14e-02, rnorm = 4.14e-02, gnorm = 4.05e-01, feval = 01066, geval = 0355
iter = 0355, obj = 4.12e-02, rnorm = 4.12e-02, gnorm = 2.55e-01, feval = 01069, geval = 0356
iter = 0356, obj = 4.10e-02, rnorm = 4.10e-02, gnorm = 4.03e-01, feval = 01072, geval = 0357
iter = 0357, obj = 4.09e-02, rnorm = 4.09e-02, gnorm = 2.53e-01, feval = 01075, geval = 0358
iter = 0358, obj = 4.07e-02, rnorm = 4.07e-02, gnorm = 4.01e-01, feval = 01078, geval = 0359
iter = 0359, obj = 4.06e-02, rnorm = 4.06e-02, gnorm = 2.52e-01, feval = 01081, geval = 0360
iter = 0360, obj = 4.04e-02, rnorm = 4.04e-02, gnorm = 3.99e-01, feval = 01084, geval = 0361
iter = 0361, obj = 4.03e-02, rnorm = 4.03e-02, gnorm = 2.51e-01, feval = 01087, geval = 0362
iter = 0362, obj = 4.01e-02, rnorm = 4.01e-02, gnorm = 3.98e-01, feval = 01090, geval = 0363
iter = 0363, obj = 3.99e-02, rnorm = 3.99e-02, gnorm = 2.50e-01, feval = 01093, geval = 0364
iter = 0364, obj = 3.98e-02, rnorm = 3.98e-02, gnorm = 3.96e-01, feval = 01096, geval = 0365
iter = 0365, obj = 3.96e-02, rnorm = 3.96e-02, gnorm = 2.49e-01, feval = 01099, geval = 0366
iter = 0366, obj = 3.95e-02, rnorm = 3.95e-02, gnorm = 3.94e-01, feval = 01102, geval = 0367
iter = 0367, obj = 3.93e-02, rnorm = 3.93e-02, gnorm = 2.48e-01, feval = 01105, geval = 0368
iter = 0368, obj = 3.92e-02, rnorm = 3.92e-02, gnorm = 3.92e-01, feval = 01108, geval = 0369
iter = 0369, obj = 3.90e-02, rnorm = 3.90e-02, gnorm = 2.47e-01, feval = 01111, geval = 0370
iter = 0370, obj = 3.89e-02, rnorm = 3.89e-02, gnorm = 3.90e-01, feval = 01114, geval = 0371
iter = 0371, obj = 3.87e-02, rnorm = 3.87e-02, gnorm = 2.45e-01, feval = 01117, geval = 0372
iter = 0372, obj = 3.86e-02, rnorm = 3.86e-02, gnorm = 3.89e-01, feval = 01120, geval = 0373
iter = 0373, obj = 3.84e-02, rnorm = 3.84e-02, gnorm = 2.44e-01, feval = 01123, geval = 0374
iter = 0374, obj = 3.83e-02, rnorm = 3.83e-02, gnorm = 3.87e-01, feval = 01126, geval = 0375
iter = 0375, obj = 3.82e-02, rnorm = 3.82e-02, gnorm = 2.43e-01, feval = 01129, geval = 0376
iter = 0376, obj = 3.80e-02, rnorm = 3.80e-02, gnorm = 3.85e-01, feval = 01132, geval = 0377
iter = 0377, obj = 3.79e-02, rnorm = 3.79e-02, gnorm = 2.42e-01, feval = 01135, geval = 0378
iter = 0378, obj = 3.77e-02, rnorm = 3.77e-02, gnorm = 3.83e-01, feval = 01138, geval = 0379
iter = 0379, obj = 3.76e-02, rnorm = 3.76e-02, gnorm = 2.41e-01, feval = 01141, geval = 0380
iter = 0380, obj = 3.74e-02, rnorm = 3.74e-02, gnorm = 3.82e-01, feval = 01144, geval = 0381
iter = 0381, obj = 3.73e-02, rnorm = 3.73e-02, gnorm = 2.40e-01, feval = 01147, geval = 0382
iter = 0382, obj = 3.72e-02, rnorm = 3.72e-02, gnorm = 3.80e-01, feval = 01150, geval = 0383
iter = 0383, obj = 3.70e-02, rnorm = 3.70e-02, gnorm = 2.39e-01, feval = 01153, geval = 0384
iter = 0384, obj = 3.69e-02, rnorm = 3.69e-02, gnorm = 3.78e-01, feval = 01156, geval = 0385
iter = 0385, obj = 3.67e-02, rnorm = 3.67e-02, gnorm = 2.38e-01, feval = 01159, geval = 0386
iter = 0386, obj = 3.66e-02, rnorm = 3.66e-02, gnorm = 3.77e-01, feval = 01162, geval = 0387
iter = 0387, obj = 3.65e-02, rnorm = 3.65e-02, gnorm = 2.37e-01, feval = 01165, geval = 0388
iter = 0388, obj = 3.63e-02, rnorm = 3.63e-02, gnorm = 3.75e-01, feval = 01168, geval = 0389
iter = 0389, obj = 3.62e-02, rnorm = 3.62e-02, gnorm = 2.36e-01, feval = 01171, geval = 0390
iter = 0390, obj = 3.61e-02, rnorm = 3.61e-02, gnorm = 3.73e-01, feval = 01174, geval = 0391
iter = 0391, obj = 3.59e-02, rnorm = 3.59e-02, gnorm = 2.35e-01, feval = 01177, geval = 0392
iter = 0392, obj = 3.58e-02, rnorm = 3.58e-02, gnorm = 3.72e-01, feval = 01180, geval = 0393
iter = 0393, obj = 3.57e-02, rnorm = 3.57e-02, gnorm = 2.34e-01, feval = 01183, geval = 0394
iter = 0394, obj = 3.55e-02, rnorm = 3.55e-02, gnorm = 3.70e-01, feval = 01186, geval = 0395
iter = 0395, obj = 3.54e-02, rnorm = 3.54e-02, gnorm = 2.33e-01, feval = 01189, geval = 0396
iter = 0396, obj = 3.53e-02, rnorm = 3.53e-02, gnorm = 3.69e-01, feval = 01192, geval = 0397
iter = 0397, obj = 3.51e-02, rnorm = 3.51e-02, gnorm = 2.32e-01, feval = 01195, geval = 0398
iter = 0398, obj = 3.50e-02, rnorm = 3.50e-02, gnorm = 3.67e-01, feval = 01198, geval = 0399
iter = 0399, obj = 3.49e-02, rnorm = 3.49e-02, gnorm = 2.31e-01, feval = 01201, geval = 0400
iter = 0400, obj = 3.47e-02, rnorm = 3.47e-02, gnorm = 3.65e-01, feval = 01204, geval = 0401
iter = 0401, obj = 3.46e-02, rnorm = 3.46e-02, gnorm = 2.30e-01, feval = 01207, geval = 0402
iter = 0402, obj = 3.45e-02, rnorm = 3.45e-02, gnorm = 3.64e-01, feval = 01210, geval = 0403
iter = 0403, obj = 3.44e-02, rnorm = 3.44e-02, gnorm = 2.29e-01, feval = 01213, geval = 0404
iter = 0404, obj = 3.42e-02, rnorm = 3.42e-02, gnorm = 3.62e-01, feval = 01216, geval = 0405
iter = 0405, obj = 3.41e-02, rnorm = 3.41e-02, gnorm = 2.28e-01, feval = 01219, geval = 0406
iter = 0406, obj = 3.40e-02, rnorm = 3.40e-02, gnorm = 3.61e-01, feval = 01222, geval = 0407
iter = 0407, obj = 3.39e-02, rnorm = 3.39e-02, gnorm = 2.27e-01, feval = 01225, geval = 0408
iter = 0408, obj = 3.37e-02, rnorm = 3.37e-02, gnorm = 3.59e-01, feval = 01228, geval = 0409
iter = 0409, obj = 3.36e-02, rnorm = 3.36e-02, gnorm = 2.26e-01, feval = 01231, geval = 0410
iter = 0410, obj = 3.35e-02, rnorm = 3.35e-02, gnorm = 3.58e-01, feval = 01234, geval = 0411
iter = 0411, obj = 3.34e-02, rnorm = 3.34e-02, gnorm = 2.25e-01, feval = 01237, geval = 0412
iter = 0412, obj = 3.33e-02, rnorm = 3.33e-02, gnorm = 3.56e-01, feval = 01240, geval = 0413
iter = 0413, obj = 3.31e-02, rnorm = 3.31e-02, gnorm = 2.24e-01, feval = 01243, geval = 0414
iter = 0414, obj = 3.30e-02, rnorm = 3.30e-02, gnorm = 3.55e-01, feval = 01246, geval = 0415
iter = 0415, obj = 3.29e-02, rnorm = 3.29e-02, gnorm = 2.23e-01, feval = 01249, geval = 0416
iter = 0416, obj = 3.28e-02, rnorm = 3.28e-02, gnorm = 3.53e-01, feval = 01252, geval = 0417
iter = 0417, obj = 3.27e-02, rnorm = 3.27e-02, gnorm = 2.22e-01, feval = 01255, geval = 0418
iter = 0418, obj = 3.25e-02, rnorm = 3.25e-02, gnorm = 3.52e-01, feval = 01258, geval = 0419
iter = 0419, obj = 3.24e-02, rnorm = 3.24e-02, gnorm = 2.21e-01, feval = 01261, geval = 0420
iter = 0420, obj = 3.23e-02, rnorm = 3.23e-02, gnorm = 3.50e-01, feval = 01264, geval = 0421

Fetching long content....

iter = 0762, obj = 1.12e-02, rnorm = 1.12e-02, gnorm = 1.93e-01, feval = 02290, geval = 0763
iter = 0763, obj = 1.11e-02, rnorm = 1.11e-02, gnorm = 1.22e-01, feval = 02293, geval = 0764
iter = 0764, obj = 1.11e-02, rnorm = 1.11e-02, gnorm = 1.92e-01, feval = 02296, geval = 0765
iter = 0765, obj = 1.11e-02, rnorm = 1.11e-02, gnorm = 1.21e-01, feval = 02299, geval = 0766
iter = 0766, obj = 1.11e-02, rnorm = 1.11e-02, gnorm = 1.92e-01, feval = 02302, geval = 0767
iter = 0767, obj = 1.10e-02, rnorm = 1.10e-02, gnorm = 1.21e-01, feval = 02305, geval = 0768
iter = 0768, obj = 1.10e-02, rnorm = 1.10e-02, gnorm = 1.91e-01, feval = 02308, geval = 0769
iter = 0769, obj = 1.10e-02, rnorm = 1.10e-02, gnorm = 1.21e-01, feval = 02311, geval = 0770
iter = 0770, obj = 1.09e-02, rnorm = 1.09e-02, gnorm = 1.90e-01, feval = 02314, geval = 0771
iter = 0771, obj = 1.09e-02, rnorm = 1.09e-02, gnorm = 1.20e-01, feval = 02317, geval = 0772
iter = 0772, obj = 1.09e-02, rnorm = 1.09e-02, gnorm = 1.90e-01, feval = 02320, geval = 0773
iter = 0773, obj = 1.08e-02, rnorm = 1.08e-02, gnorm = 1.20e-01, feval = 02323, geval = 0774
iter = 0774, obj = 1.08e-02, rnorm = 1.08e-02, gnorm = 1.89e-01, feval = 02326, geval = 0775
iter = 0775, obj = 1.08e-02, rnorm = 1.08e-02, gnorm = 1.20e-01, feval = 02329, geval = 0776
iter = 0776, obj = 1.08e-02, rnorm = 1.08e-02, gnorm = 1.89e-01, feval = 02332, geval = 0777
iter = 0777, obj = 1.07e-02, rnorm = 1.07e-02, gnorm = 1.19e-01, feval = 02335, geval = 0778
iter = 0778, obj = 1.07e-02, rnorm = 1.07e-02, gnorm = 1.88e-01, feval = 02338, geval = 0779
iter = 0779, obj = 1.07e-02, rnorm = 1.07e-02, gnorm = 1.19e-01, feval = 02341, geval = 0780
iter = 0780, obj = 1.06e-02, rnorm = 1.06e-02, gnorm = 1.88e-01, feval = 02344, geval = 0781
iter = 0781, obj = 1.06e-02, rnorm = 1.06e-02, gnorm = 1.19e-01, feval = 02347, geval = 0782
iter = 0782, obj = 1.06e-02, rnorm = 1.06e-02, gnorm = 1.87e-01, feval = 02350, geval = 0783
iter = 0783, obj = 1.05e-02, rnorm = 1.05e-02, gnorm = 1.18e-01, feval = 02353, geval = 0784
iter = 0784, obj = 1.05e-02, rnorm = 1.05e-02, gnorm = 1.86e-01, feval = 02356, geval = 0785
iter = 0785, obj = 1.05e-02, rnorm = 1.05e-02, gnorm = 1.18e-01, feval = 02359, geval = 0786
iter = 0786, obj = 1.05e-02, rnorm = 1.05e-02, gnorm = 1.86e-01, feval = 02362, geval = 0787
iter = 0787, obj = 1.04e-02, rnorm = 1.04e-02, gnorm = 1.17e-01, feval = 02365, geval = 0788
iter = 0788, obj = 1.04e-02, rnorm = 1.04e-02, gnorm = 1.85e-01, feval = 02368, geval = 0789
iter = 0789, obj = 1.04e-02, rnorm = 1.04e-02, gnorm = 1.17e-01, feval = 02371, geval = 0790
iter = 0790, obj = 1.03e-02, rnorm = 1.03e-02, gnorm = 1.85e-01, feval = 02374, geval = 0791
iter = 0791, obj = 1.03e-02, rnorm = 1.03e-02, gnorm = 1.17e-01, feval = 02377, geval = 0792
iter = 0792, obj = 1.03e-02, rnorm = 1.03e-02, gnorm = 1.84e-01, feval = 02380, geval = 0793
iter = 0793, obj = 1.03e-02, rnorm = 1.03e-02, gnorm = 1.16e-01, feval = 02383, geval = 0794
iter = 0794, obj = 1.02e-02, rnorm = 1.02e-02, gnorm = 1.84e-01, feval = 02386, geval = 0795
iter = 0795, obj = 1.02e-02, rnorm = 1.02e-02, gnorm = 1.16e-01, feval = 02389, geval = 0796
iter = 0796, obj = 1.02e-02, rnorm = 1.02e-02, gnorm = 1.83e-01, feval = 02392, geval = 0797
iter = 0797, obj = 1.02e-02, rnorm = 1.02e-02, gnorm = 1.16e-01, feval = 02395, geval = 0798
iter = 0798, obj = 1.01e-02, rnorm = 1.01e-02, gnorm = 1.83e-01, feval = 02398, geval = 0799
iter = 0799, obj = 1.01e-02, rnorm = 1.01e-02, gnorm = 1.15e-01, feval = 02401, geval = 0800
iter = 0800, obj = 1.01e-02, rnorm = 1.01e-02, gnorm = 1.82e-01, feval = 02404, geval = 0801
iter = 0801, obj = 1.00e-02, rnorm = 1.00e-02, gnorm = 1.15e-01, feval = 02407, geval = 0802
iter = 0802, obj = 1.00e-02, rnorm = 1.00e-02, gnorm = 1.82e-01, feval = 02410, geval = 0803
iter = 0803, obj = 9.99e-03, rnorm = 9.99e-03, gnorm = 1.15e-01, feval = 02413, geval = 0804
iter = 0804, obj = 9.96e-03, rnorm = 9.96e-03, gnorm = 1.81e-01, feval = 02416, geval = 0805
iter = 0805, obj = 9.94e-03, rnorm = 9.94e-03, gnorm = 1.14e-01, feval = 02419, geval = 0806
iter = 0806, obj = 9.91e-03, rnorm = 9.91e-03, gnorm = 1.80e-01, feval = 02422, geval = 0807
iter = 0807, obj = 9.88e-03, rnorm = 9.88e-03, gnorm = 1.14e-01, feval = 02425, geval = 0808
iter = 0808, obj = 9.86e-03, rnorm = 9.86e-03, gnorm = 1.80e-01, feval = 02428, geval = 0809
iter = 0809, obj = 9.83e-03, rnorm = 9.83e-03, gnorm = 1.14e-01, feval = 02431, geval = 0810
iter = 0810, obj = 9.80e-03, rnorm = 9.80e-03, gnorm = 1.79e-01, feval = 02434, geval = 0811
iter = 0811, obj = 9.78e-03, rnorm = 9.78e-03, gnorm = 1.13e-01, feval = 02437, geval = 0812
iter = 0812, obj = 9.75e-03, rnorm = 9.75e-03, gnorm = 1.79e-01, feval = 02440, geval = 0813
iter = 0813, obj = 9.72e-03, rnorm = 9.72e-03, gnorm = 1.13e-01, feval = 02443, geval = 0814
iter = 0814, obj = 9.70e-03, rnorm = 9.70e-03, gnorm = 1.78e-01, feval = 02446, geval = 0815
iter = 0815, obj = 9.67e-03, rnorm = 9.67e-03, gnorm = 1.13e-01, feval = 02449, geval = 0816
iter = 0816, obj = 9.64e-03, rnorm = 9.64e-03, gnorm = 1.78e-01, feval = 02452, geval = 0817
iter = 0817, obj = 9.62e-03, rnorm = 9.62e-03, gnorm = 1.12e-01, feval = 02455, geval = 0818
iter = 0818, obj = 9.59e-03, rnorm = 9.59e-03, gnorm = 1.77e-01, feval = 02458, geval = 0819
iter = 0819, obj = 9.57e-03, rnorm = 9.57e-03, gnorm = 1.12e-01, feval = 02461, geval = 0820
iter = 0820, obj = 9.54e-03, rnorm = 9.54e-03, gnorm = 1.77e-01, feval = 02464, geval = 0821
iter = 0821, obj = 9.52e-03, rnorm = 9.52e-03, gnorm = 1.12e-01, feval = 02467, geval = 0822
iter = 0822, obj = 9.49e-03, rnorm = 9.49e-03, gnorm = 1.76e-01, feval = 02470, geval = 0823
iter = 0823, obj = 9.46e-03, rnorm = 9.46e-03, gnorm = 1.11e-01, feval = 02473, geval = 0824
iter = 0824, obj = 9.44e-03, rnorm = 9.44e-03, gnorm = 1.76e-01, feval = 02476, geval = 0825
iter = 0825, obj = 9.41e-03, rnorm = 9.41e-03, gnorm = 1.11e-01, feval = 02479, geval = 0826
iter = 0826, obj = 9.39e-03, rnorm = 9.39e-03, gnorm = 1.75e-01, feval = 02482, geval = 0827
iter = 0827, obj = 9.36e-03, rnorm = 9.36e-03, gnorm = 1.11e-01, feval = 02485, geval = 0828
iter = 0828, obj = 9.34e-03, rnorm = 9.34e-03, gnorm = 1.75e-01, feval = 02488, geval = 0829
iter = 0829, obj = 9.31e-03, rnorm = 9.31e-03, gnorm = 1.10e-01, feval = 02491, geval = 0830
iter = 0830, obj = 9.29e-03, rnorm = 9.29e-03, gnorm = 1.74e-01, feval = 02494, geval = 0831
iter = 0831, obj = 9.26e-03, rnorm = 9.26e-03, gnorm = 1.10e-01, feval = 02497, geval = 0832
iter = 0832, obj = 9.24e-03, rnorm = 9.24e-03, gnorm = 1.74e-01, feval = 02500, geval = 0833
iter = 0833, obj = 9.21e-03, rnorm = 9.21e-03, gnorm = 1.10e-01, feval = 02503, geval = 0834
iter = 0834, obj = 9.19e-03, rnorm = 9.19e-03, gnorm = 1.73e-01, feval = 02506, geval = 0835
iter = 0835, obj = 9.16e-03, rnorm = 9.16e-03, gnorm = 1.10e-01, feval = 02509, geval = 0836
iter = 0836, obj = 9.14e-03, rnorm = 9.14e-03, gnorm = 1.73e-01, feval = 02512, geval = 0837
iter = 0837, obj = 9.12e-03, rnorm = 9.12e-03, gnorm = 1.09e-01, feval = 02515, geval = 0838
iter = 0838, obj = 9.09e-03, rnorm = 9.09e-03, gnorm = 1.72e-01, feval = 02518, geval = 0839
iter = 0839, obj = 9.07e-03, rnorm = 9.07e-03, gnorm = 1.09e-01, feval = 02521, geval = 0840
iter = 0840, obj = 9.04e-03, rnorm = 9.04e-03, gnorm = 1.72e-01, feval = 02524, geval = 0841
iter = 0841, obj = 9.02e-03, rnorm = 9.02e-03, gnorm = 1.09e-01, feval = 02527, geval = 0842
iter = 0842, obj = 9.00e-03, rnorm = 9.00e-03, gnorm = 1.71e-01, feval = 02530, geval = 0843
iter = 0843, obj = 8.97e-03, rnorm = 8.97e-03, gnorm = 1.08e-01, feval = 02533, geval = 0844
iter = 0844, obj = 8.95e-03, rnorm = 8.95e-03, gnorm = 1.71e-01, feval = 02536, geval = 0845
iter = 0845, obj = 8.92e-03, rnorm = 8.92e-03, gnorm = 1.08e-01, feval = 02539, geval = 0846
iter = 0846, obj = 8.90e-03, rnorm = 8.90e-03, gnorm = 1.70e-01, feval = 02542, geval = 0847
iter = 0847, obj = 8.88e-03, rnorm = 8.88e-03, gnorm = 1.08e-01, feval = 02545, geval = 0848
iter = 0848, obj = 8.85e-03, rnorm = 8.85e-03, gnorm = 1.70e-01, feval = 02548, geval = 0849
iter = 0849, obj = 8.83e-03, rnorm = 8.83e-03, gnorm = 1.07e-01, feval = 02551, geval = 0850
iter = 0850, obj = 8.81e-03, rnorm = 8.81e-03, gnorm = 1.69e-01, feval = 02554, geval = 0851
iter = 0851, obj = 8.78e-03, rnorm = 8.78e-03, gnorm = 1.07e-01, feval = 02557, geval = 0852
iter = 0852, obj = 8.76e-03, rnorm = 8.76e-03, gnorm = 1.69e-01, feval = 02560, geval = 0853
iter = 0853, obj = 8.74e-03, rnorm = 8.74e-03, gnorm = 1.07e-01, feval = 02563, geval = 0854
iter = 0854, obj = 8.71e-03, rnorm = 8.71e-03, gnorm = 1.68e-01, feval = 02566, geval = 0855
iter = 0855, obj = 8.69e-03, rnorm = 8.69e-03, gnorm = 1.06e-01, feval = 02569, geval = 0856
iter = 0856, obj = 8.67e-03, rnorm = 8.67e-03, gnorm = 1.68e-01, feval = 02572, geval = 0857
iter = 0857, obj = 8.64e-03, rnorm = 8.64e-03, gnorm = 1.06e-01, feval = 02575, geval = 0858
iter = 0858, obj = 8.62e-03, rnorm = 8.62e-03, gnorm = 1.67e-01, feval = 02578, geval = 0859
iter = 0859, obj = 8.60e-03, rnorm = 8.60e-03, gnorm = 1.06e-01, feval = 02581, geval = 0860
iter = 0860, obj = 8.58e-03, rnorm = 8.58e-03, gnorm = 1.67e-01, feval = 02584, geval = 0861
iter = 0861, obj = 8.55e-03, rnorm = 8.55e-03, gnorm = 1.06e-01, feval = 02587, geval = 0862
iter = 0862, obj = 8.53e-03, rnorm = 8.53e-03, gnorm = 1.66e-01, feval = 02590, geval = 0863
iter = 0863, obj = 8.51e-03, rnorm = 8.51e-03, gnorm = 1.05e-01, feval = 02593, geval = 0864
iter = 0864, obj = 8.48e-03, rnorm = 8.48e-03, gnorm = 1.66e-01, feval = 02596, geval = 0865
iter = 0865, obj = 8.46e-03, rnorm = 8.46e-03, gnorm = 1.05e-01, feval = 02599, geval = 0866
iter = 0866, obj = 8.44e-03, rnorm = 8.44e-03, gnorm = 1.65e-01, feval = 02602, geval = 0867
iter = 0867, obj = 8.42e-03, rnorm = 8.42e-03, gnorm = 1.05e-01, feval = 02605, geval = 0868
iter = 0868, obj = 8.40e-03, rnorm = 8.40e-03, gnorm = 1.65e-01, feval = 02608, geval = 0869
iter = 0869, obj = 8.37e-03, rnorm = 8.37e-03, gnorm = 1.04e-01, feval = 02611, geval = 0870
iter = 0870, obj = 8.35e-03, rnorm = 8.35e-03, gnorm = 1.65e-01, feval = 02614, geval = 0871
iter = 0871, obj = 8.33e-03, rnorm = 8.33e-03, gnorm = 1.04e-01, feval = 02617, geval = 0872
iter = 0872, obj = 8.31e-03, rnorm = 8.31e-03, gnorm = 1.64e-01, feval = 02620, geval = 0873
iter = 0873, obj = 8.29e-03, rnorm = 8.29e-03, gnorm = 1.04e-01, feval = 02623, geval = 0874
iter = 0874, obj = 8.26e-03, rnorm = 8.26e-03, gnorm = 1.64e-01, feval = 02626, geval = 0875
iter = 0875, obj = 8.24e-03, rnorm = 8.24e-03, gnorm = 1.03e-01, feval = 02629, geval = 0876
iter = 0876, obj = 8.22e-03, rnorm = 8.22e-03, gnorm = 1.63e-01, feval = 02632, geval = 0877
iter = 0877, obj = 8.20e-03, rnorm = 8.20e-03, gnorm = 1.03e-01, feval = 02635, geval = 0878
iter = 0878, obj = 8.18e-03, rnorm = 8.18e-03, gnorm = 1.63e-01, feval = 02638, geval = 0879
iter = 0879, obj = 8.16e-03, rnorm = 8.16e-03, gnorm = 1.03e-01, feval = 02641, geval = 0880
iter = 0880, obj = 8.13e-03, rnorm = 8.13e-03, gnorm = 1.62e-01, feval = 02644, geval = 0881
iter = 0881, obj = 8.11e-03, rnorm = 8.11e-03, gnorm = 1.03e-01, feval = 02647, geval = 0882
iter = 0882, obj = 8.09e-03, rnorm = 8.09e-03, gnorm = 1.62e-01, feval = 02650, geval = 0883
iter = 0883, obj = 8.07e-03, rnorm = 8.07e-03, gnorm = 1.02e-01, feval = 02653, geval = 0884
iter = 0884, obj = 8.05e-03, rnorm = 8.05e-03, gnorm = 1.61e-01, feval = 02656, geval = 0885
iter = 0885, obj = 8.03e-03, rnorm = 8.03e-03, gnorm = 1.02e-01, feval = 02659, geval = 0886
iter = 0886, obj = 8.01e-03, rnorm = 8.01e-03, gnorm = 1.61e-01, feval = 02662, geval = 0887
iter = 0887, obj = 7.99e-03, rnorm = 7.99e-03, gnorm = 1.02e-01, feval = 02665, geval = 0888
iter = 0888, obj = 7.97e-03, rnorm = 7.97e-03, gnorm = 1.60e-01, feval = 02668, geval = 0889
iter = 0889, obj = 7.95e-03, rnorm = 7.95e-03, gnorm = 1.01e-01, feval = 02671, geval = 0890
iter = 0890, obj = 7.92e-03, rnorm = 7.92e-03, gnorm = 1.60e-01, feval = 02674, geval = 0891
iter = 0891, obj = 7.90e-03, rnorm = 7.90e-03, gnorm = 1.01e-01, feval = 02677, geval = 0892
iter = 0892, obj = 7.88e-03, rnorm = 7.88e-03, gnorm = 1.59e-01, feval = 02680, geval = 0893
iter = 0893, obj = 7.86e-03, rnorm = 7.86e-03, gnorm = 1.01e-01, feval = 02683, geval = 0894
iter = 0894, obj = 7.84e-03, rnorm = 7.84e-03, gnorm = 1.59e-01, feval = 02686, geval = 0895
iter = 0895, obj = 7.82e-03, rnorm = 7.82e-03, gnorm = 1.01e-01, feval = 02689, geval = 0896
iter = 0896, obj = 7.80e-03, rnorm = 7.80e-03, gnorm = 1.59e-01, feval = 02692, geval = 0897
iter = 0897, obj = 7.78e-03, rnorm = 7.78e-03, gnorm = 1.00e-01, feval = 02695, geval = 0898
iter = 0898, obj = 7.76e-03, rnorm = 7.76e-03, gnorm = 1.58e-01, feval = 02698, geval = 0899
iter = 0899, obj = 7.74e-03, rnorm = 7.74e-03, gnorm = 1.00e-01, feval = 02701, geval = 0900
iter = 0900, obj = 7.72e-03, rnorm = 7.72e-03, gnorm = 1.58e-01, feval = 02704, geval = 0901
iter = 0901, obj = 7.70e-03, rnorm = 7.70e-03, gnorm = 9.97e-02, feval = 02707, geval = 0902
iter = 0902, obj = 7.68e-03, rnorm = 7.68e-03, gnorm = 1.57e-01, feval = 02710, geval = 0903
iter = 0903, obj = 7.66e-03, rnorm = 7.66e-03, gnorm = 9.94e-02, feval = 02713, geval = 0904
iter = 0904, obj = 7.64e-03, rnorm = 7.64e-03, gnorm = 1.57e-01, feval = 02716, geval = 0905
iter = 0905, obj = 7.62e-03, rnorm = 7.62e-03, gnorm = 9.92e-02, feval = 02719, geval = 0906
iter = 0906, obj = 7.60e-03, rnorm = 7.60e-03, gnorm = 1.56e-01, feval = 02722, geval = 0907
iter = 0907, obj = 7.58e-03, rnorm = 7.58e-03, gnorm = 9.89e-02, feval = 02725, geval = 0908
iter = 0908, obj = 7.56e-03, rnorm = 7.56e-03, gnorm = 1.56e-01, feval = 02728, geval = 0909
iter = 0909, obj = 7.54e-03, rnorm = 7.54e-03, gnorm = 9.86e-02, feval = 02731, geval = 0910
iter = 0910, obj = 7.52e-03, rnorm = 7.52e-03, gnorm = 1.56e-01, feval = 02734, geval = 0911
iter = 0911, obj = 7.50e-03, rnorm = 7.50e-03, gnorm = 9.83e-02, feval = 02737, geval = 0912
iter = 0912, obj = 7.48e-03, rnorm = 7.48e-03, gnorm = 1.55e-01, feval = 02740, geval = 0913
iter = 0913, obj = 7.46e-03, rnorm = 7.46e-03, gnorm = 9.81e-02, feval = 02743, geval = 0914
iter = 0914, obj = 7.44e-03, rnorm = 7.44e-03, gnorm = 1.55e-01, feval = 02746, geval = 0915
iter = 0915, obj = 7.43e-03, rnorm = 7.43e-03, gnorm = 9.78e-02, feval = 02749, geval = 0916
iter = 0916, obj = 7.41e-03, rnorm = 7.41e-03, gnorm = 1.54e-01, feval = 02752, geval = 0917
iter = 0917, obj = 7.39e-03, rnorm = 7.39e-03, gnorm = 9.75e-02, feval = 02755, geval = 0918
iter = 0918, obj = 7.37e-03, rnorm = 7.37e-03, gnorm = 1.54e-01, feval = 02758, geval = 0919
iter = 0919, obj = 7.35e-03, rnorm = 7.35e-03, gnorm = 9.73e-02, feval = 02761, geval = 0920
iter = 0920, obj = 7.33e-03, rnorm = 7.33e-03, gnorm = 1.53e-01, feval = 02764, geval = 0921
iter = 0921, obj = 7.31e-03, rnorm = 7.31e-03, gnorm = 9.70e-02, feval = 02767, geval = 0922
iter = 0922, obj = 7.29e-03, rnorm = 7.29e-03, gnorm = 1.53e-01, feval = 02770, geval = 0923
iter = 0923, obj = 7.27e-03, rnorm = 7.27e-03, gnorm = 9.67e-02, feval = 02773, geval = 0924
iter = 0924, obj = 7.25e-03, rnorm = 7.25e-03, gnorm = 1.53e-01, feval = 02776, geval = 0925
iter = 0925, obj = 7.24e-03, rnorm = 7.24e-03, gnorm = 9.65e-02, feval = 02779, geval = 0926
iter = 0926, obj = 7.22e-03, rnorm = 7.22e-03, gnorm = 1.52e-01, feval = 02782, geval = 0927
iter = 0927, obj = 7.20e-03, rnorm = 7.20e-03, gnorm = 9.62e-02, feval = 02785, geval = 0928
iter = 0928, obj = 7.18e-03, rnorm = 7.18e-03, gnorm = 1.52e-01, feval = 02788, geval = 0929
iter = 0929, obj = 7.16e-03, rnorm = 7.16e-03, gnorm = 9.59e-02, feval = 02791, geval = 0930
iter = 0930, obj = 7.14e-03, rnorm = 7.14e-03, gnorm = 1.51e-01, feval = 02794, geval = 0931
iter = 0931, obj = 7.13e-03, rnorm = 7.13e-03, gnorm = 9.57e-02, feval = 02797, geval = 0932
iter = 0932, obj = 7.11e-03, rnorm = 7.11e-03, gnorm = 1.51e-01, feval = 02800, geval = 0933
iter = 0933, obj = 7.09e-03, rnorm = 7.09e-03, gnorm = 9.54e-02, feval = 02803, geval = 0934
iter = 0934, obj = 7.07e-03, rnorm = 7.07e-03, gnorm = 1.50e-01, feval = 02806, geval = 0935
iter = 0935, obj = 7.05e-03, rnorm = 7.05e-03, gnorm = 9.51e-02, feval = 02809, geval = 0936
iter = 0936, obj = 7.03e-03, rnorm = 7.03e-03, gnorm = 1.50e-01, feval = 02812, geval = 0937
iter = 0937, obj = 7.02e-03, rnorm = 7.02e-03, gnorm = 9.49e-02, feval = 02815, geval = 0938
iter = 0938, obj = 7.00e-03, rnorm = 7.00e-03, gnorm = 1.50e-01, feval = 02818, geval = 0939
iter = 0939, obj = 6.98e-03, rnorm = 6.98e-03, gnorm = 9.46e-02, feval = 02821, geval = 0940
iter = 0940, obj = 6.96e-03, rnorm = 6.96e-03, gnorm = 1.49e-01, feval = 02824, geval = 0941
iter = 0941, obj = 6.94e-03, rnorm = 6.94e-03, gnorm = 9.44e-02, feval = 02827, geval = 0942
iter = 0942, obj = 6.93e-03, rnorm = 6.93e-03, gnorm = 1.49e-01, feval = 02830, geval = 0943
iter = 0943, obj = 6.91e-03, rnorm = 6.91e-03, gnorm = 9.41e-02, feval = 02833, geval = 0944
iter = 0944, obj = 6.89e-03, rnorm = 6.89e-03, gnorm = 1.48e-01, feval = 02836, geval = 0945
iter = 0945, obj = 6.87e-03, rnorm = 6.87e-03, gnorm = 9.38e-02, feval = 02839, geval = 0946
iter = 0946, obj = 6.86e-03, rnorm = 6.86e-03, gnorm = 1.48e-01, feval = 02842, geval = 0947
iter = 0947, obj = 6.84e-03, rnorm = 6.84e-03, gnorm = 9.36e-02, feval = 02845, geval = 0948
iter = 0948, obj = 6.82e-03, rnorm = 6.82e-03, gnorm = 1.48e-01, feval = 02848, geval = 0949
iter = 0949, obj = 6.80e-03, rnorm = 6.80e-03, gnorm = 9.33e-02, feval = 02851, geval = 0950
iter = 0950, obj = 6.79e-03, rnorm = 6.79e-03, gnorm = 1.47e-01, feval = 02854, geval = 0951
iter = 0951, obj = 6.77e-03, rnorm = 6.77e-03, gnorm = 9.31e-02, feval = 02857, geval = 0952
iter = 0952, obj = 6.75e-03, rnorm = 6.75e-03, gnorm = 1.47e-01, feval = 02860, geval = 0953
iter = 0953, obj = 6.73e-03, rnorm = 6.73e-03, gnorm = 9.28e-02, feval = 02863, geval = 0954
iter = 0954, obj = 6.72e-03, rnorm = 6.72e-03, gnorm = 1.46e-01, feval = 02866, geval = 0955
iter = 0955, obj = 6.70e-03, rnorm = 6.70e-03, gnorm = 9.26e-02, feval = 02869, geval = 0956
iter = 0956, obj = 6.68e-03, rnorm = 6.68e-03, gnorm = 1.46e-01, feval = 02872, geval = 0957
iter = 0957, obj = 6.67e-03, rnorm = 6.67e-03, gnorm = 9.23e-02, feval = 02875, geval = 0958
iter = 0958, obj = 6.65e-03, rnorm = 6.65e-03, gnorm = 1.46e-01, feval = 02878, geval = 0959
iter = 0959, obj = 6.63e-03, rnorm = 6.63e-03, gnorm = 9.21e-02, feval = 02881, geval = 0960
iter = 0960, obj = 6.62e-03, rnorm = 6.62e-03, gnorm = 1.45e-01, feval = 02884, geval = 0961
iter = 0961, obj = 6.60e-03, rnorm = 6.60e-03, gnorm = 9.18e-02, feval = 02887, geval = 0962
iter = 0962, obj = 6.58e-03, rnorm = 6.58e-03, gnorm = 1.45e-01, feval = 02890, geval = 0963
iter = 0963, obj = 6.57e-03, rnorm = 6.57e-03, gnorm = 9.16e-02, feval = 02893, geval = 0964
iter = 0964, obj = 6.55e-03, rnorm = 6.55e-03, gnorm = 1.44e-01, feval = 02896, geval = 0965
iter = 0965, obj = 6.53e-03, rnorm = 6.53e-03, gnorm = 9.13e-02, feval = 02899, geval = 0966
iter = 0966, obj = 6.52e-03, rnorm = 6.52e-03, gnorm = 1.44e-01, feval = 02902, geval = 0967
iter = 0967, obj = 6.50e-03, rnorm = 6.50e-03, gnorm = 9.11e-02, feval = 02905, geval = 0968
iter = 0968, obj = 6.48e-03, rnorm = 6.48e-03, gnorm = 1.44e-01, feval = 02908, geval = 0969
iter = 0969, obj = 6.47e-03, rnorm = 6.47e-03, gnorm = 9.08e-02, feval = 02911, geval = 0970
iter = 0970, obj = 6.45e-03, rnorm = 6.45e-03, gnorm = 1.43e-01, feval = 02914, geval = 0971
iter = 0971, obj = 6.43e-03, rnorm = 6.43e-03, gnorm = 9.06e-02, feval = 02917, geval = 0972
iter = 0972, obj = 6.42e-03, rnorm = 6.42e-03, gnorm = 1.43e-01, feval = 02920, geval = 0973
iter = 0973, obj = 6.40e-03, rnorm = 6.40e-03, gnorm = 9.03e-02, feval = 02923, geval = 0974
iter = 0974, obj = 6.38e-03, rnorm = 6.38e-03, gnorm = 1.42e-01, feval = 02926, geval = 0975
iter = 0975, obj = 6.37e-03, rnorm = 6.37e-03, gnorm = 9.01e-02, feval = 02929, geval = 0976
iter = 0976, obj = 6.35e-03, rnorm = 6.35e-03, gnorm = 1.42e-01, feval = 02932, geval = 0977
iter = 0977, obj = 6.34e-03, rnorm = 6.34e-03, gnorm = 8.98e-02, feval = 02935, geval = 0978
iter = 0978, obj = 6.32e-03, rnorm = 6.32e-03, gnorm = 1.42e-01, feval = 02938, geval = 0979
iter = 0979, obj = 6.30e-03, rnorm = 6.30e-03, gnorm = 8.96e-02, feval = 02941, geval = 0980
iter = 0980, obj = 6.29e-03, rnorm = 6.29e-03, gnorm = 1.41e-01, feval = 02944, geval = 0981
iter = 0981, obj = 6.27e-03, rnorm = 6.27e-03, gnorm = 8.94e-02, feval = 02947, geval = 0982
iter = 0982, obj = 6.26e-03, rnorm = 6.26e-03, gnorm = 1.41e-01, feval = 02950, geval = 0983
iter = 0983, obj = 6.24e-03, rnorm = 6.24e-03, gnorm = 8.91e-02, feval = 02953, geval = 0984
iter = 0984, obj = 6.22e-03, rnorm = 6.22e-03, gnorm = 1.40e-01, feval = 02956, geval = 0985
iter = 0985, obj = 6.21e-03, rnorm = 6.21e-03, gnorm = 8.89e-02, feval = 02959, geval = 0986
iter = 0986, obj = 6.19e-03, rnorm = 6.19e-03, gnorm = 1.40e-01, feval = 02962, geval = 0987
iter = 0987, obj = 6.18e-03, rnorm = 6.18e-03, gnorm = 8.86e-02, feval = 02965, geval = 0988
iter = 0988, obj = 6.16e-03, rnorm = 6.16e-03, gnorm = 1.40e-01, feval = 02968, geval = 0989
iter = 0989, obj = 6.15e-03, rnorm = 6.15e-03, gnorm = 8.84e-02, feval = 02971, geval = 0990
iter = 0990, obj = 6.13e-03, rnorm = 6.13e-03, gnorm = 1.39e-01, feval = 02974, geval = 0991
iter = 0991, obj = 6.12e-03, rnorm = 6.12e-03, gnorm = 8.82e-02, feval = 02977, geval = 0992
iter = 0992, obj = 6.10e-03, rnorm = 6.10e-03, gnorm = 1.39e-01, feval = 02980, geval = 0993
iter = 0993, obj = 6.09e-03, rnorm = 6.09e-03, gnorm = 8.79e-02, feval = 02983, geval = 0994
iter = 0994, obj = 6.07e-03, rnorm = 6.07e-03, gnorm = 1.39e-01, feval = 02986, geval = 0995
iter = 0995, obj = 6.05e-03, rnorm = 6.05e-03, gnorm = 8.77e-02, feval = 02989, geval = 0996
iter = 0996, obj = 6.04e-03, rnorm = 6.04e-03, gnorm = 1.38e-01, feval = 02992, geval = 0997
iter = 0997, obj = 6.02e-03, rnorm = 6.02e-03, gnorm = 8.75e-02, feval = 02995, geval = 0998
iter = 0998, obj = 6.01e-03, rnorm = 6.01e-03, gnorm = 1.38e-01, feval = 02998, geval = 0999
iter = 0999, obj = 5.99e-03, rnorm = 5.99e-03, gnorm = 8.72e-02, feval = 03001, geval = 1000
iter = 1000, obj = 5.98e-03, rnorm = 5.98e-03, gnorm = 1.38e-01, feval = 03004, geval = 1001
Terminate: maximum number of iterations reached

##########################################################################################
    Nonlinear SD Solver end
##########################################################################################

Let's again plot the optimization path. In this case, the algorithm finds only falls close to the vicinity of the global minimum but does not reach even after 1000 iteration. In the figure below, we can see that the algorithm is sampling most of the objective function within the parabolic valley.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle(r"Nonlinear Steepest Descent")

plt.show()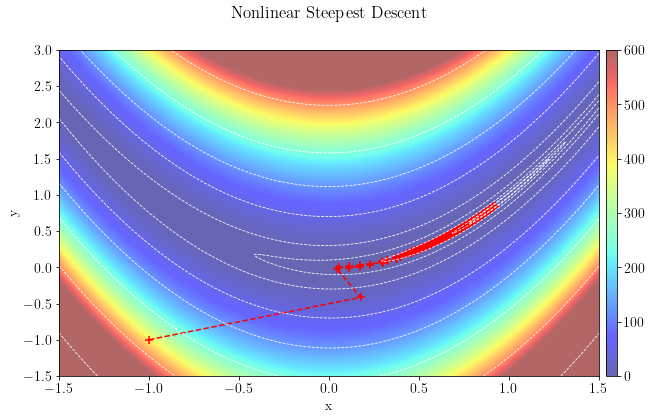

In the third test, let's apply the BFGS algorithm to find the function's global minimum.

ParabStep = o.ParabolicStep()
BFGSsolver = o.LBFGS(Stop, stepper=ParabStep)
Ros_prob = Rosenbrock(x_init, y_init)
BFGSsolver.setDefaults(save_obj=True, save_model=True)
BFGSsolver.run(Ros_prob, verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSsolver.model)):
    x_smpld.append(BFGSsolver.model[i][0])
    y_smpld.append(BFGSsolver.model[i][1])

##########################################################################################
            BFGS Solver 
    Restart folder: /tmp/restart_2022-04-22T01-49-08.932818/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 4.01e+01, rnorm = 4.01e+01, gnorm = 1.33e+02, feval = 00004, geval = 0002
iter = 0002, obj = 1.47e+00, rnorm = 1.47e+00, gnorm = 1.50e+01, feval = 00007, geval = 0003
iter = 0003, obj = 8.58e-01, rnorm = 8.58e-01, gnorm = 2.09e+00, feval = 00010, geval = 0004
iter = 0004, obj = 8.50e-01, rnorm = 8.50e-01, gnorm = 2.01e+00, feval = 00013, geval = 0005
iter = 0005, obj = 7.40e-01, rnorm = 7.40e-01, gnorm = 8.34e+00, feval = 00016, geval = 0006
iter = 0006, obj = 6.72e-01, rnorm = 6.72e-01, gnorm = 2.65e+00, feval = 00019, geval = 0007
iter = 0007, obj = 5.62e-01, rnorm = 5.62e-01, gnorm = 2.40e+00, feval = 00022, geval = 0008
iter = 0008, obj = 4.63e-01, rnorm = 4.63e-01, gnorm = 4.76e+00, feval = 00025, geval = 0009
iter = 0009, obj = 3.26e-01, rnorm = 3.26e-01, gnorm = 7.06e+00, feval = 00028, geval = 0010
iter = 0010, obj = 2.30e-01, rnorm = 2.30e-01, gnorm = 2.06e+00, feval = 00031, geval = 0011
iter = 0011, obj = 1.55e-01, rnorm = 1.55e-01, gnorm = 3.36e+00, feval = 00034, geval = 0012
iter = 0012, obj = 1.32e-01, rnorm = 1.32e-01, gnorm = 6.11e+00, feval = 00037, geval = 0013
iter = 0013, obj = 5.41e-02, rnorm = 5.41e-02, gnorm = 2.37e+00, feval = 00040, geval = 0014
iter = 0014, obj = 3.17e-02, rnorm = 3.17e-02, gnorm = 2.19e+00, feval = 00043, geval = 0015
iter = 0015, obj = 2.24e-02, rnorm = 2.24e-02, gnorm = 3.84e+00, feval = 00046, geval = 0016
iter = 0016, obj = 6.53e-03, rnorm = 6.53e-03, gnorm = 1.20e+00, feval = 00049, geval = 0017
iter = 0017, obj = 2.15e-03, rnorm = 2.15e-03, gnorm = 4.75e-01, feval = 00052, geval = 0018
iter = 0018, obj = 1.21e-03, rnorm = 1.21e-03, gnorm = 1.04e+00, feval = 00055, geval = 0019
iter = 0019, obj = 8.24e-06, rnorm = 8.24e-06, gnorm = 7.00e-02, feval = 00058, geval = 0020
iter = 0020, obj = 4.57e-08, rnorm = 4.57e-08, gnorm = 7.87e-03, feval = 00061, geval = 0021
iter = 0021, obj = 4.19e-12, rnorm = 4.19e-12, gnorm = 5.98e-05, feval = 00064, geval = 0022
iter = 0022, obj = 2.21e-17, rnorm = 2.21e-17, gnorm = 1.59e-07, feval = 00067, geval = 0023
iter = 0023, obj = 1.46e-29, rnorm = 1.46e-29, gnorm = 9.38e-14, feval = 00070, geval = 0024
iter = 0024, obj = 0.00e+00, rnorm = 0.00e+00, gnorm = 0.00e+00, feval = 00073, geval = 0025
Terminate: minimum residual tolerance reached 0.0

##########################################################################################
            BFGS Solver end
##########################################################################################

The algorithm has precisely reached the global minimum in 24 iterations. We can clearly see that it is able to find an approximation of the local curvature of the objective function. In fact, it needs to sample very few points within the parabolic-shaped valley.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle("L-BFGS with Parabolic stepper")
plt.show()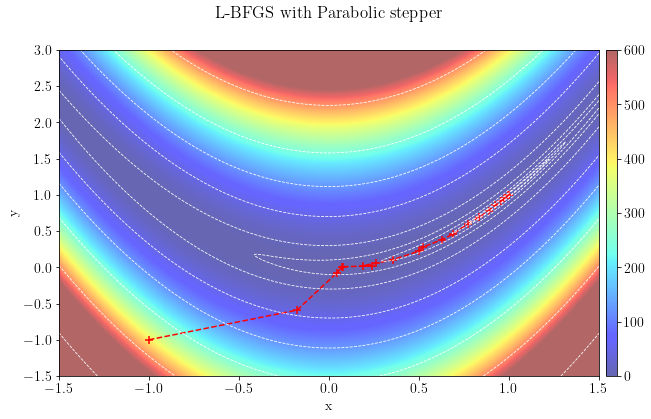

Let's try to solve the same problem using the Strong-Wolfe stepper described by Nocedal and Wright (1999) in the Algorithm 3.2 on page 59.

WolfeStep = o.StrongWolfe(alpha=0.0) #We now use a stepper that satisfies the strong Wolfe conditions
BFGSsolver = o.LBFGS(Stop, stepper=WolfeStep)
Ros_prob = Rosenbrock(x_init, y_init) #Resetting the problem
BFGSsolver.setDefaults(save_obj=True, save_model=True)
BFGSsolver.run(Ros_prob, verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSsolver.model)):
    x_smpld.append(BFGSsolver.model[i][0])
    y_smpld.append(BFGSsolver.model[i][1])

##########################################################################################
            BFGS Solver 
    Restart folder: /tmp/restart_2022-04-22T01-49-09.683188/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 1.36e+02, rnorm = 1.36e+02, gnorm = 3.63e+02, feval = 00002, geval = 0002
iter = 0002, obj = 5.54e+01, rnorm = 5.54e+01, gnorm = 1.81e+02, feval = 00003, geval = 0003
iter = 0003, obj = 1.77e+01, rnorm = 1.77e+01, gnorm = 8.53e+01, feval = 00004, geval = 0004
iter = 0004, obj = 4.91e+00, rnorm = 4.91e+00, gnorm = 3.96e+01, feval = 00005, geval = 0005
iter = 0005, obj = 1.35e+00, rnorm = 1.35e+00, gnorm = 1.43e+01, feval = 00006, geval = 0006
iter = 0006, obj = 7.80e-01, rnorm = 7.80e-01, gnorm = 2.83e+00, feval = 00007, geval = 0007
iter = 0007, obj = 7.39e-01, rnorm = 7.39e-01, gnorm = 2.13e+00, feval = 00008, geval = 0008
iter = 0008, obj = 7.34e-01, rnorm = 7.34e-01, gnorm = 2.62e+00, feval = 00009, geval = 0009
iter = 0009, obj = 7.22e-01, rnorm = 7.22e-01, gnorm = 3.58e+00, feval = 00010, geval = 0010
iter = 0010, obj = 6.81e-01, rnorm = 6.81e-01, gnorm = 5.32e+00, feval = 00011, geval = 0011
iter = 0011, obj = 3.22e-01, rnorm = 3.22e-01, gnorm = 5.63e+00, feval = 00015, geval = 0014
iter = 0012, obj = 3.14e-01, rnorm = 3.14e-01, gnorm = 2.06e+00, feval = 00021, geval = 0018
iter = 0013, obj = 3.07e-01, rnorm = 3.07e-01, gnorm = 2.85e+00, feval = 00022, geval = 0019
iter = 0014, obj = 2.90e-01, rnorm = 2.90e-01, gnorm = 4.79e+00, feval = 00023, geval = 0020
iter = 0015, obj = 2.71e-01, rnorm = 2.71e-01, gnorm = 5.13e+00, feval = 00024, geval = 0021
iter = 0016, obj = 1.88e-01, rnorm = 1.88e-01, gnorm = 4.83e+00, feval = 00025, geval = 0022
iter = 0017, obj = 1.23e-01, rnorm = 1.23e-01, gnorm = 1.65e+00, feval = 00026, geval = 0023
iter = 0018, obj = 9.99e-02, rnorm = 9.99e-02, gnorm = 7.40e+00, feval = 00027, geval = 0024
iter = 0019, obj = 5.62e-02, rnorm = 5.62e-02, gnorm = 3.45e-01, feval = 00028, geval = 0025
iter = 0020, obj = 3.27e-02, rnorm = 3.27e-02, gnorm = 1.03e+00, feval = 00029, geval = 0026
iter = 0021, obj = 2.24e-02, rnorm = 2.24e-02, gnorm = 3.22e+00, feval = 00033, geval = 0029
iter = 0022, obj = 1.22e-02, rnorm = 1.22e-02, gnorm = 1.73e+00, feval = 00034, geval = 0030
iter = 0023, obj = 4.45e-03, rnorm = 4.45e-03, gnorm = 1.38e+00, feval = 00035, geval = 0031
iter = 0024, obj = 1.87e-03, rnorm = 1.87e-03, gnorm = 9.34e-01, feval = 00036, geval = 0032
iter = 0025, obj = 2.43e-04, rnorm = 2.43e-04, gnorm = 3.08e-02, feval = 00040, geval = 0035
iter = 0026, obj = 8.38e-05, rnorm = 8.38e-05, gnorm = 4.05e-01, feval = 00041, geval = 0036
iter = 0027, obj = 1.38e-05, rnorm = 1.38e-05, gnorm = 1.11e-01, feval = 00042, geval = 0037
iter = 0028, obj = 8.59e-07, rnorm = 8.59e-07, gnorm = 7.34e-03, feval = 00043, geval = 0038
iter = 0029, obj = 8.33e-09, rnorm = 8.33e-09, gnorm = 1.25e-03, feval = 00044, geval = 0039
iter = 0030, obj = 6.56e-12, rnorm = 6.56e-12, gnorm = 1.10e-04, feval = 00045, geval = 0040
iter = 0031, obj = 1.58e-14, rnorm = 1.58e-14, gnorm = 5.37e-06, feval = 00046, geval = 0041
iter = 0032, obj = 2.05e-18, rnorm = 2.05e-18, gnorm = 2.02e-08, feval = 00047, geval = 0042
iter = 0033, obj = 2.27e-22, rnorm = 2.27e-22, gnorm = 1.97e-10, feval = 00048, geval = 0043
iter = 0034, obj = 1.45e-27, rnorm = 1.45e-27, gnorm = 1.61e-12, feval = 00049, geval = 0044
iter = 0035, obj = 0.00e+00, rnorm = 0.00e+00, gnorm = 0.00e+00, feval = 00050, geval = 0045
Terminate: minimum residual tolerance reached 0.0

##########################################################################################
            BFGS Solver end
##########################################################################################

The BFGS algorithm combined with this specific stepper reached the objective function's minimum in 35 iterations with 50 and 45 function and gradient evaluations, respectively.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle("L-BFGS with Strong-Wolfe stepper")
plt.show()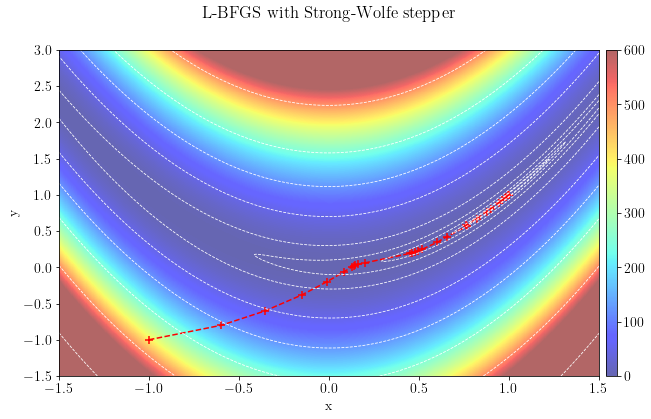

Finally, let's test again the BFGS method but this time employing the line-search algorithm proposed by More and Thuente (1994). Their line-search method uses a backeting approach in which the strong Wolfe conditions are verified for the tested point. In this case, if these conditons are met, then the method was successful.

BFGSsolver = o.LBFGS(Stop)
Ros_prob = Rosenbrock(x_init, y_init)
BFGSsolver.setDefaults(save_obj=True, save_model=True)
BFGSsolver.run(Ros_prob, verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSsolver.model)):
    x_smpld.append(BFGSsolver.model[i][0])
    y_smpld.append(BFGSsolver.model[i][1])

##########################################################################################
            BFGS Solver 
    Restart folder: /tmp/restart_2022-04-22T01-49-10.348843/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 1.36e+02, rnorm = 1.36e+02, gnorm = 3.63e+02, feval = 00002, geval = 0002
iter = 0002, obj = 5.54e+01, rnorm = 5.54e+01, gnorm = 1.81e+02, feval = 00003, geval = 0003
iter = 0003, obj = 1.77e+01, rnorm = 1.77e+01, gnorm = 8.53e+01, feval = 00004, geval = 0004
iter = 0004, obj = 4.91e+00, rnorm = 4.91e+00, gnorm = 3.96e+01, feval = 00005, geval = 0005
iter = 0005, obj = 1.35e+00, rnorm = 1.35e+00, gnorm = 1.43e+01, feval = 00006, geval = 0006
iter = 0006, obj = 7.80e-01, rnorm = 7.80e-01, gnorm = 2.83e+00, feval = 00007, geval = 0007
iter = 0007, obj = 7.39e-01, rnorm = 7.39e-01, gnorm = 2.13e+00, feval = 00008, geval = 0008
iter = 0008, obj = 7.34e-01, rnorm = 7.34e-01, gnorm = 2.62e+00, feval = 00009, geval = 0009
iter = 0009, obj = 7.22e-01, rnorm = 7.22e-01, gnorm = 3.58e+00, feval = 00010, geval = 0010
iter = 0010, obj = 6.81e-01, rnorm = 6.81e-01, gnorm = 5.32e+00, feval = 00011, geval = 0011
iter = 0011, obj = 4.48e-01, rnorm = 4.48e-01, gnorm = 4.93e+00, feval = 00013, geval = 0013
iter = 0012, obj = 3.44e-01, rnorm = 3.44e-01, gnorm = 7.88e+00, feval = 00015, geval = 0015
iter = 0013, obj = 3.27e-01, rnorm = 3.27e-01, gnorm = 9.22e-01, feval = 00016, geval = 0016
iter = 0014, obj = 3.06e-01, rnorm = 3.06e-01, gnorm = 2.16e+00, feval = 00017, geval = 0017
iter = 0015, obj = 2.97e-01, rnorm = 2.97e-01, gnorm = 3.90e+00, feval = 00018, geval = 0018
iter = 0016, obj = 2.88e-01, rnorm = 2.88e-01, gnorm = 4.12e+00, feval = 00019, geval = 0019
iter = 0017, obj = 2.12e-01, rnorm = 2.12e-01, gnorm = 5.93e+00, feval = 00020, geval = 0020
iter = 0018, obj = 1.51e-01, rnorm = 1.51e-01, gnorm = 2.91e+00, feval = 00021, geval = 0021
iter = 0019, obj = 9.89e-02, rnorm = 9.89e-02, gnorm = 4.74e+00, feval = 00022, geval = 0022
iter = 0020, obj = 5.25e-02, rnorm = 5.25e-02, gnorm = 1.23e+00, feval = 00023, geval = 0023
iter = 0021, obj = 3.21e-02, rnorm = 3.21e-02, gnorm = 1.95e+00, feval = 00025, geval = 0025
iter = 0022, obj = 2.47e-02, rnorm = 2.47e-02, gnorm = 4.13e+00, feval = 00026, geval = 0026
iter = 0023, obj = 1.23e-02, rnorm = 1.23e-02, gnorm = 1.39e+00, feval = 00027, geval = 0027
iter = 0024, obj = 4.28e-03, rnorm = 4.28e-03, gnorm = 1.01e+00, feval = 00028, geval = 0028
iter = 0025, obj = 1.24e-03, rnorm = 1.24e-03, gnorm = 6.41e-01, feval = 00029, geval = 0029
iter = 0026, obj = 2.09e-04, rnorm = 2.09e-04, gnorm = 4.02e-02, feval = 00030, geval = 0030
iter = 0027, obj = 6.58e-05, rnorm = 6.58e-05, gnorm = 2.64e-01, feval = 00032, geval = 0032
iter = 0028, obj = 1.33e-06, rnorm = 1.33e-06, gnorm = 3.02e-02, feval = 00033, geval = 0033
iter = 0029, obj = 8.24e-09, rnorm = 8.24e-09, gnorm = 2.62e-03, feval = 00034, geval = 0034
iter = 0030, obj = 3.58e-12, rnorm = 3.58e-12, gnorm = 2.41e-05, feval = 00035, geval = 0035
iter = 0031, obj = 7.73e-14, rnorm = 7.73e-14, gnorm = 9.42e-06, feval = 00036, geval = 0036
iter = 0032, obj = 2.67e-17, rnorm = 2.67e-17, gnorm = 2.17e-07, feval = 00037, geval = 0037
iter = 0033, obj = 1.73e-20, rnorm = 1.73e-20, gnorm = 3.78e-09, feval = 00038, geval = 0038
iter = 0034, obj = 1.91e-25, rnorm = 1.91e-25, gnorm = 7.10e-12, feval = 00039, geval = 0039
iter = 0035, obj = 3.01e-30, rnorm = 3.01e-30, gnorm = 5.20e-14, feval = 00040, geval = 0040
iter = 0036, obj = 0.00e+00, rnorm = 0.00e+00, gnorm = 0.00e+00, feval = 00041, geval = 0041
Terminate: minimum residual tolerance reached 0.0

##########################################################################################
            BFGS Solver end
##########################################################################################

We can see that the algorithm has reached the global minimum in 36 iterations. However, since we employed a different stepping method, in which no parabolic interpolation is used during the optimization, the algorithm had to perfom only 41 objective function evaluations as opposed to 73 necessary by the BFGS method when the parabolic stepper was the line-search algorithm of choice.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle("L-BFGS with CvSrch stepper")

plt.show()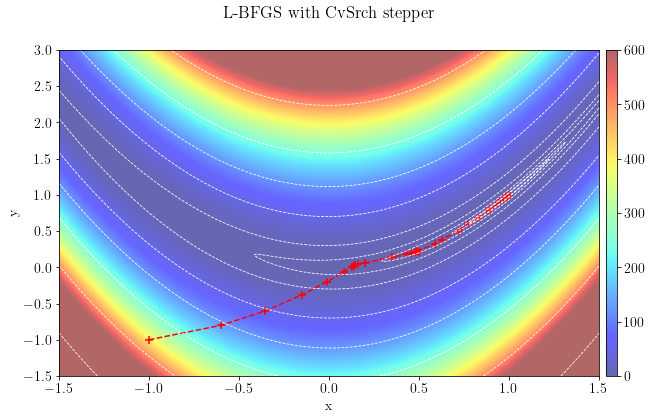

Constrained non-linear optimization¶

We now try to solve the save non-linear problem but we impose maximum and minimum boundary conditions as follows:

\begin{equation} \phi(x,y) = (1-x)^2 + 100 (y-x^2)^2,\\ \text{s.t.} \; x_l \leq x \leq x_m \; \text{and} \; y_l \leq y \leq y_m \end{equation}

(2)

where $x_l$ , $y_l$ , $x_m$ , and $y_m$ represent the minimum and maximum allowed values for each optimization variable, respectively. Let's first define a problem object with two bound vectors having the inequality conditions shown in the previous equations. To solve such problem, we employ the L-BFGS-B algorithm proposed by Byrd et al. (1995). Let's try with some bounds that contains the global minimum of the objective function.

# Lower and upper bounds and associtated vectors
xl, yl = -1.2, -1.2
xu, yu = 1.2, 2.0
minBound = o.VectorNumpy(np.array((xl, yl)))
maxBound = o.VectorNumpy(np.array((xu, yu)))

Stop  = o.BasicStopper(niter=1000, tolg_proj=1e-32)
BFGSBsolver = o.LBFGSB(Stop, m_steps=10)
Ros_prob = Rosenbrock(x_init, y_init, minBound, maxBound)
BFGSBsolver.setDefaults(save_obj=True, save_model=True)
BFGSBsolver.run(Ros_prob,verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSBsolver.model)):
    x_smpld.append(BFGSBsolver.model[i][0])
    y_smpld.append(BFGSBsolver.model[i][1])

# Setting bounds for plotting
bounds_points_x = np.array([minBound[0],minBound[0],maxBound[0],maxBound[0],minBound[0]])
bounds_points_y = np.array([minBound[1],maxBound[1],maxBound[1],minBound[1],minBound[1]])

##########################################################################################
            L-BFGS-B Solver 
    Max steps to invert the Hessian: 10 
    Restart folder: /tmp/restart_2022-04-22T01-49-11.102678/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 1.50e+01, rnorm = 1.50e+01, gnorm = 9.49e+01, feval = 00002, geval = 0002
iter = 0002, obj = 4.26e+00, rnorm = 4.26e+00, gnorm = 3.98e+01, feval = 00003, geval = 0003
iter = 0003, obj = 1.74e+00, rnorm = 1.74e+00, gnorm = 3.77e+00, feval = 00004, geval = 0004
iter = 0004, obj = 1.72e+00, rnorm = 1.72e+00, gnorm = 2.38e+00, feval = 00005, geval = 0005
iter = 0005, obj = 1.67e+00, rnorm = 1.67e+00, gnorm = 2.60e+00, feval = 00006, geval = 0006
iter = 0006, obj = 1.07e+00, rnorm = 1.07e+00, gnorm = 6.68e+00, feval = 00015, geval = 0012
iter = 0007, obj = 1.04e+00, rnorm = 1.04e+00, gnorm = 2.62e+00, feval = 00019, geval = 0015
iter = 0008, obj = 9.78e-01, rnorm = 9.78e-01, gnorm = 4.07e+00, feval = 00020, geval = 0016
iter = 0009, obj = 7.42e-01, rnorm = 7.42e-01, gnorm = 3.90e+00, feval = 00029, geval = 0022
iter = 0010, obj = 7.34e-01, rnorm = 7.34e-01, gnorm = 2.14e+00, feval = 00037, geval = 0027
iter = 0011, obj = 7.19e-01, rnorm = 7.19e-01, gnorm = 2.49e+00, feval = 00038, geval = 0028
iter = 0012, obj = 3.96e-01, rnorm = 3.96e-01, gnorm = 1.18e+00, feval = 00045, geval = 0033
iter = 0013, obj = 3.96e-01, rnorm = 3.96e-01, gnorm = 1.03e+00, feval = 00065, geval = 0044
iter = 0014, obj = 3.91e-01, rnorm = 3.91e-01, gnorm = 1.36e+00, feval = 00066, geval = 0045
iter = 0015, obj = 3.60e-01, rnorm = 3.60e-01, gnorm = 2.38e+00, feval = 00067, geval = 0046
iter = 0016, obj = 3.24e-01, rnorm = 3.24e-01, gnorm = 3.66e+00, feval = 00068, geval = 0047
iter = 0017, obj = 2.98e-01, rnorm = 2.98e-01, gnorm = 2.18e+00, feval = 00069, geval = 0048
iter = 0018, obj = 2.62e-01, rnorm = 2.62e-01, gnorm = 1.30e+00, feval = 00070, geval = 0049
iter = 0019, obj = 2.13e-01, rnorm = 2.13e-01, gnorm = 1.52e+00, feval = 00071, geval = 0050
iter = 0020, obj = 1.88e-01, rnorm = 1.88e-01, gnorm = 2.44e+00, feval = 00075, geval = 0053
iter = 0021, obj = 1.61e-01, rnorm = 1.61e-01, gnorm = 4.57e+00, feval = 00079, geval = 0056
iter = 0022, obj = 1.31e-01, rnorm = 1.31e-01, gnorm = 3.29e+00, feval = 00080, geval = 0057
iter = 0023, obj = 8.30e-02, rnorm = 8.30e-02, gnorm = 5.20e+00, feval = 00081, geval = 0058
iter = 0024, obj = 6.76e-02, rnorm = 6.76e-02, gnorm = 6.89e-01, feval = 00085, geval = 0061
iter = 0025, obj = 5.46e-02, rnorm = 5.46e-02, gnorm = 9.65e-01, feval = 00086, geval = 0062
iter = 0026, obj = 4.51e-02, rnorm = 4.51e-02, gnorm = 3.30e+00, feval = 00090, geval = 0065
iter = 0027, obj = 3.50e-02, rnorm = 3.50e-02, gnorm = 1.33e+00, feval = 00091, geval = 0066
iter = 0028, obj = 2.83e-02, rnorm = 2.83e-02, gnorm = 1.16e+00, feval = 00092, geval = 0067
iter = 0029, obj = 1.11e-02, rnorm = 1.11e-02, gnorm = 2.36e+00, feval = 00093, geval = 0068
iter = 0030, obj = 4.65e-03, rnorm = 4.65e-03, gnorm = 6.64e-01, feval = 00099, geval = 0072
iter = 0031, obj = 3.33e-03, rnorm = 3.33e-03, gnorm = 2.13e+00, feval = 00100, geval = 0073
iter = 0032, obj = 1.68e-03, rnorm = 1.68e-03, gnorm = 4.29e-01, feval = 00101, geval = 0074
iter = 0033, obj = 1.10e-03, rnorm = 1.10e-03, gnorm = 5.41e-01, feval = 00102, geval = 0075
iter = 0034, obj = 6.57e-04, rnorm = 6.57e-04, gnorm = 7.47e-01, feval = 00103, geval = 0076
iter = 0035, obj = 4.14e-04, rnorm = 4.14e-04, gnorm = 3.34e-01, feval = 00104, geval = 0077
iter = 0036, obj = 1.95e-04, rnorm = 1.95e-04, gnorm = 1.63e-01, feval = 00105, geval = 0078
iter = 0037, obj = 4.68e-05, rnorm = 4.68e-05, gnorm = 1.21e-01, feval = 00106, geval = 0079
iter = 0038, obj = 1.33e-05, rnorm = 1.33e-05, gnorm = 8.52e-02, feval = 00107, geval = 0080
iter = 0039, obj = 5.76e-07, rnorm = 5.76e-07, gnorm = 2.33e-02, feval = 00108, geval = 0081
iter = 0040, obj = 2.52e-09, rnorm = 2.52e-09, gnorm = 1.96e-03, feval = 00109, geval = 0082
iter = 0041, obj = 9.05e-13, rnorm = 9.05e-13, gnorm = 7.53e-06, feval = 00110, geval = 0083
iter = 0042, obj = 5.82e-15, rnorm = 5.82e-15, gnorm = 1.89e-06, feval = 00111, geval = 0084
iter = 0043, obj = 2.18e-17, rnorm = 2.18e-17, gnorm = 1.81e-07, feval = 00112, geval = 0085
iter = 0044, obj = 2.04e-20, rnorm = 2.04e-20, gnorm = 6.35e-09, feval = 00113, geval = 0086
iter = 0045, obj = 5.45e-24, rnorm = 5.45e-24, gnorm = 9.77e-11, feval = 00114, geval = 0087
iter = 0046, obj = 9.22e-27, rnorm = 9.22e-27, gnorm = 9.67e-13, feval = 00115, geval = 0088
iter = 0047, obj = 1.51e-29, rnorm = 1.51e-29, gnorm = 7.77e-15, feval = 00116, geval = 0089
iter = 0048, obj = 0.00e+00, rnorm = 0.00e+00, gnorm = 0.00e+00, feval = 00117, geval = 0090
Terminate: minimum residual tolerance reached 0.0

##########################################################################################
            L-BFGS-B Solver end
##########################################################################################

The method is able to reach the global minimum since it is contianed within the provided bounds (plotted with white dashed segments).

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

ax.scatter(bounds_points_x, bounds_points_y, marker="o", color='w', s=30)
ax.plot(bounds_points_x, bounds_points_y, "--", color='w', linewidth=2)

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle(r"L-BFGS-B with %s upper bound" % maxBound[:].tolist())
plt.show()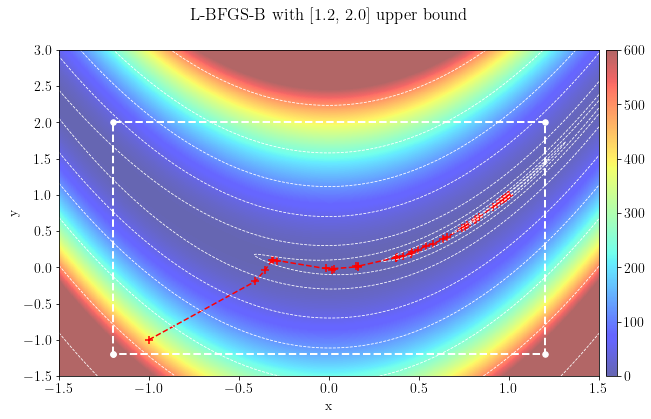

Let's now try to reduce the upper bounds and see where the method stops.

# Lower and upper bounds and associtated vectors
xl, yl = -1.2, -1.2
xu, yu = 0.5, 1.0
minBound = o.VectorNumpy(np.array((xl, yl)))
maxBound = o.VectorNumpy(np.array((xu, yu)))

Stop  = o.BasicStopper(niter=1000, tolg_proj=1e-32)
BFGSBsolver = o.LBFGSB(Stop, m_steps=10)
Ros_prob = Rosenbrock(x_init, y_init, minBound, maxBound)
BFGSBsolver.setDefaults(save_obj=True, save_model=True)
BFGSBsolver.run(Ros_prob,verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSBsolver.model)):
    x_smpld.append(BFGSBsolver.model[i][0])
    y_smpld.append(BFGSBsolver.model[i][1])

# Setting bounds for plotting
bounds_points_x = np.array([minBound[0],minBound[0],maxBound[0],maxBound[0],minBound[0]])
bounds_points_y = np.array([minBound[1],maxBound[1],maxBound[1],minBound[1],minBound[1]])

##########################################################################################
            L-BFGS-B Solver 
    Max steps to invert the Hessian: 10 
    Restart folder: /tmp/restart_2022-04-22T01-49-11.781368/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 1.49e+01, rnorm = 1.49e+01, gnorm = 9.40e+01, feval = 00002, geval = 0002
iter = 0002, obj = 4.33e+00, rnorm = 4.33e+00, gnorm = 4.02e+01, feval = 00003, geval = 0003
iter = 0003, obj = 1.72e+00, rnorm = 1.72e+00, gnorm = 3.79e+00, feval = 00004, geval = 0004
iter = 0004, obj = 1.69e+00, rnorm = 1.69e+00, gnorm = 2.37e+00, feval = 00005, geval = 0005
iter = 0005, obj = 1.64e+00, rnorm = 1.64e+00, gnorm = 2.59e+00, feval = 00006, geval = 0006
iter = 0006, obj = 1.05e+00, rnorm = 1.05e+00, gnorm = 5.78e+00, feval = 00013, geval = 0011
iter = 0007, obj = 1.02e+00, rnorm = 1.02e+00, gnorm = 3.00e+00, feval = 00017, geval = 0014
iter = 0008, obj = 9.64e-01, rnorm = 9.64e-01, gnorm = 4.19e+00, feval = 00018, geval = 0015
iter = 0009, obj = 6.12e-01, rnorm = 6.12e-01, gnorm = 2.93e+00, feval = 00023, geval = 0019
iter = 0010, obj = 6.09e-01, rnorm = 6.09e-01, gnorm = 1.77e+00, feval = 00035, geval = 0026
iter = 0011, obj = 5.66e-01, rnorm = 5.66e-01, gnorm = 4.81e+00, feval = 00042, geval = 0031
iter = 0012, obj = 5.39e-01, rnorm = 5.39e-01, gnorm = 1.30e+00, feval = 00043, geval = 0032
iter = 0013, obj = 5.30e-01, rnorm = 5.30e-01, gnorm = 1.66e+00, feval = 00044, geval = 0033
iter = 0014, obj = 4.84e-01, rnorm = 4.84e-01, gnorm = 6.62e+00, feval = 00049, geval = 0037
iter = 0015, obj = 4.41e-01, rnorm = 4.41e-01, gnorm = 1.11e+00, feval = 00050, geval = 0038
iter = 0016, obj = 4.01e-01, rnorm = 4.01e-01, gnorm = 2.02e+00, feval = 00051, geval = 0039
iter = 0017, obj = 3.73e-01, rnorm = 3.73e-01, gnorm = 3.04e+00, feval = 00052, geval = 0040
iter = 0018, obj = 3.48e-01, rnorm = 3.48e-01, gnorm = 2.45e+00, feval = 00053, geval = 0041
iter = 0019, obj = 2.60e-01, rnorm = 2.60e-01, gnorm = 2.28e+00, feval = 00054, geval = 0042
iter = 0020, obj = 2.52e-01, rnorm = 2.52e-01, gnorm = 9.96e-01, feval = 00055, geval = 0043
iter = 0021, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.60e-01, feval = 00056, geval = 0044
iter = 0022, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.27e-01, feval = 00057, geval = 0045
iter = 0023, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.12e-01, feval = 00058, geval = 0046
iter = 0024, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.07e-01, feval = 00059, geval = 0047
iter = 0025, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.07e-01, feval = 00060, geval = 0048
iter = 0026, obj = 2.51e-01, rnorm = 2.51e-01, gnorm = 7.07e-01, feval = 00061, geval = 0049
##########################################################################################
            L-BFGS-B Solver end
##########################################################################################

The algorithm reaches the closest feasible minimum point as we can see from the plot below. This point is indeed positioned at on of the boundary.

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

ax.scatter(bounds_points_x, bounds_points_y, marker="o", color='w', s=30)
ax.plot(bounds_points_x, bounds_points_y, "--", color='w', linewidth=2)

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle(r"L-BFGS-B with %s upper bound" % maxBound[:].tolist())
plt.show()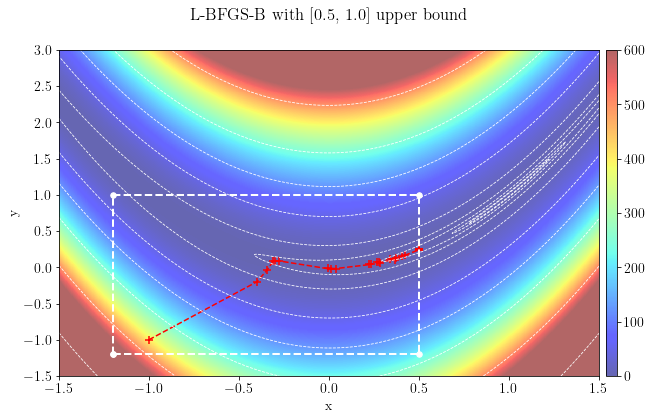

# Lower and upper bounds and associtated vectors
xl, yl = -1.2, -1.2
xu, yu = 0., 0.
minBound = o.VectorNumpy(np.array((xl, yl)))
maxBound = o.VectorNumpy(np.array((xu, yu)))

Stop  = o.BasicStopper(niter=1000, tolg_proj=1e-32)
BFGSBsolver = o.LBFGSB(Stop, m_steps=10)
Ros_prob = Rosenbrock(x_init, y_init, minBound, maxBound) #Resetting the problem
BFGSBsolver.setDefaults(save_obj=True, save_model=True)
BFGSBsolver.run(Ros_prob,verbose=True)

# Converting sampled points to arrays for plotting
x_smpld = []
y_smpld = []
for i in range(len(BFGSBsolver.model)):
    x_smpld.append(BFGSBsolver.model[i][0])
    y_smpld.append(BFGSBsolver.model[i][1])

# Setting bounds for plotting
bounds_points_x = np.array([minBound[0],minBound[0],maxBound[0],maxBound[0],minBound[0]])
bounds_points_y = np.array([minBound[1],maxBound[1],maxBound[1],minBound[1],minBound[1]])

##########################################################################################
            L-BFGS-B Solver 
    Max steps to invert the Hessian: 10 
    Restart folder: /tmp/restart_2022-04-22T01-49-12.773562/
##########################################################################################

iter = 0000, obj = 4.04e+02, rnorm = 4.04e+02, gnorm = 8.98e+02, feval = 00001, geval = 0001
iter = 0001, obj = 1.60e+01, rnorm = 1.60e+01, gnorm = 8.91e+01, feval = 00002, geval = 0002
iter = 0002, obj = 5.87e+00, rnorm = 5.87e+00, gnorm = 4.73e+01, feval = 00003, geval = 0003
iter = 0003, obj = 1.44e+00, rnorm = 1.44e+00, gnorm = 7.00e+00, feval = 00004, geval = 0004
iter = 0004, obj = 1.44e+00, rnorm = 1.44e+00, gnorm = 7.00e+00, feval = 00005, geval = 0005
iter = 0005, obj = 1.44e+00, rnorm = 1.44e+00, gnorm = 7.00e+00, feval = 00006, geval = 0006
iter = 0006, obj = 1.44e+00, rnorm = 1.44e+00, gnorm = 7.00e+00, feval = 00007, geval = 0007
iter = 0007, obj = 1.08e+00, rnorm = 1.08e+00, gnorm = 2.38e+00, feval = 00008, geval = 0008
iter = 0008, obj = 1.00e+00, rnorm = 1.00e+00, gnorm = 2.00e+00, feval = 00009, geval = 0009
Terminate: tolerance of the projected gradient reached 0.0

##########################################################################################
            L-BFGS-B Solver end
##########################################################################################

fig, ax = plt.subplots()

ax.scatter(x_smpld, y_smpld, color='red', s=50, marker="+")
ax.plot(x_smpld, y_smpld, "--", color='red')

ax.scatter(bounds_points_x, bounds_points_y, marker="o", color='w', s=30)
ax.plot(bounds_points_x, bounds_points_y, "--", color='w', linewidth=2)

im = ax.imshow(obj_ros.plot().T, alpha=0.6, clim=(0,600), extent=[1.5,-1.5,-1.5,3.0])
ax.set_xlabel("x"), ax.set_ylabel("y")
ax.invert_xaxis()

cs = plt.contour(obj_ros.plot().T,
                 levels=[0.05,0.1,0.5,2,10,50,125,250,500,1000],
                 extent=[-1.5,1.5,3.0,-1.5],
                 colors="white", linewidths=(0.8,), linestyles='--')
divider = make_axes_locatable(ax)
plt.colorbar(im, cax=divider.append_axes("right", size="2%", pad=0.1))
plt.suptitle(r"L-BFGS-B with %s upper bound" % maxBound[:].tolist())
plt.show()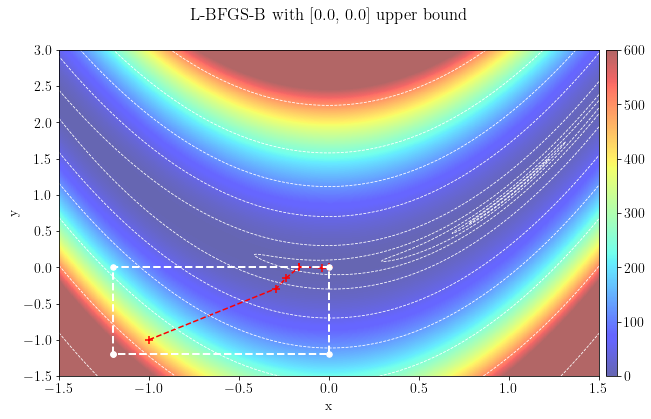

Again, the method is able to reach the closest feasible minimum of the objective function.

Notebooks

2D Travel-time tomography using the Eikonal equation

Notebooks

Traveltime tomography for Seismic Exploration

Rosenbrock: a nonlinear problem survey

Testing non-linear solvers on the Rosenbrock function¶

Problem definition¶

Instantiation of the inverse problem and of the various solvers¶

Constrained non-linear optimization¶