Simple quadratic convex problems¶

@Author: Ettore Biondi - ebiondi@caltech.edu

Instantiation of vectors and operator¶

For testing the library we will be using a discretized version of the following operator:

\begin{align} y = \frac{d^2f(x)}{dx^2}, \end{align}

(1)

in which we simply compute the second-order derivative of a function $f(x)$ .

Importing necessary libraries¶

import numpy as np
import occamypy as o

# Plotting
from matplotlib import rcParams
from mpl_toolkits.axes_grid1 import make_axes_locatable
import matplotlib.pyplot as plt
rcParams.update({
    'image.cmap'     : 'gray',
    'image.aspect'   : 'auto',
    'image.interpolation': None,
    'axes.grid'      : True,
    'figure.figsize' : (6, 4),
    'savefig.dpi'    : 300,
    'axes.labelsize' : 14,
    'axes.titlesize' : 16,
    'font.size'      : 14,
    'legend.fontsize': 14,
    'xtick.labelsize': 14,
    'ytick.labelsize': 14,
    'text.usetex'    : True,
    'font.family'    : 'serif',
    'font.serif'     : 'Latin Modern Roman',
})

WARNING! DATAPATH not found. The folder /tmp will be used to write binary files

/nas/home/fpicetti/miniconda3/envs/occd/lib/python3.10/site-packages/dask_jobqueue/core.py:20: FutureWarning: tmpfile is deprecated and will be removed in a future release. Please use dask.utils.tmpfile instead.
  from distributed.utils import tmpfile

N = 200  # Number of points of the function f(x)
dx = 1/N  # Sampling of the function

# The stencil used is simply: (f(ix-1)-2f(ix)+f(ix+1))/(dx*dx)
D2 = np.zeros((N, N), dtype=np.float64)
np.fill_diagonal(D2, -2 / (dx * dx))
np.fill_diagonal(D2[1:], 1 / (dx * dx))
np.fill_diagonal(D2[:,1:], 1 / (dx * dx))

f = o.VectorNumpy((N, 1)).zero()
y = f.clone()

D2 = o.Matrix(o.VectorNumpy(D2), f, y)

Before we set any inversion problem, we study some of the properties of the constructed operator Deriv2Op.

# Verifying operator adjointness through dot-product test
D2.dotTest(verbose=True)

Dot-product tests of forward and adjoint operators
--------------------------------------------------
Applying forward operator add=False
 Runs in: 0.004538536071777344 seconds
Applying adjoint operator add=False
 Runs in: 0.0005342960357666016 seconds
Dot products add=False: domain=2.381674e+05 range=2.381674e+05 
Absolute error: 5.820766e-11
Relative error: 2.443982e-16 

Applying forward operator add=True
 Runs in: 7.200241088867188e-05 seconds
Applying adjoint operator add=True
 Runs in: 0.00022292137145996094 seconds
Dot products add=True: domain=4.763347e+05 range=4.763347e+05 
Absolute error: 1.164153e-10
Relative error: 2.443982e-16 

-------------------------------------------------

Computing maximum and minimum eigenvalues of the operator using the power iteration method and compare them against the ones computed using numpy

egsOp = D2.powerMethod(verbose=False, eval_min=True, tol=1e-300)
egsNp, _ = np.linalg.eig(D2.matrix.getNdArray())
egsNp = egsNp[egsNp.argsort()[::-1]] #Sorting the eigenvalues
print("\nMaximum eigenvalue: %s (Power method), %s (NUMPY)" % (egsOp[0], egsNp[-1]))
print(  "Minimum eigenvalue: %s (Power method), %s (NUMPY)" % (egsOp[1], egsNp[0]))


Maximum eigenvalue: -159990.22855475376 (Power method), -159990.2285552523 (NUMPY)
Minimum eigenvalue: -9.771445230813697 (Power method), -9.77144474784679 (NUMPY)

We can see that the matrix is negative definite. The small mismatch in the estimated eigenvalues is due to the dependence of the power method on the initial random eigenvector.

Inversion tests¶

We will now focus our attention on inverting a function knowning its second-order derivative. In this case we will assume that $y$ is constant and equal to $1$ . Therefore, we expect to obtain a parabola with positive curvature. Given the chosen boundary conditions we know that the matrix is invertible since all eigenvalues have the same sign and are different then zero. We will solve the following objective functions using linear conjugate-gradient methods:

\begin{equation*} \phi_1(\mathbf{f}) = \frac{1}{2}\|D_2\mathbf{f}-\mathbf{y}\|_2^2 \end{equation*}

(2)

and

\begin{equation*} \phi_2(\mathbf{f}) = \frac{1}{2}\mathbf{f}^T D_2 \mathbf{f} - \mathbf{f}^{T} \mathbf{y}, \end{equation*}

(3)

where $D_2$ represents the discretized second-order derivative operator, while $\mathbf{f}$ and $\mathbf{y}$ are the discretized representations of $f$ and $y$ , respectively.

y.set(1.) # y = 1
# Note that f = 0
Phi1 = o.LeastSquares(f.clone().zero(), y, D2)
Phi2 = o.LeastSquaresSymmetric(f.clone().zero(), y, D2)

Instantiation of solver objects¶

First, we create two different solver object for solving the two inversion problem stated above.

# Create LCG solver
LCGsolver = o.CG(o.BasicStopper(niter=2000))
LCGsolver.setDefaults(save_obj=True)

# Create LCG solver for symmetric systems
SLCG = o.CGsym(o.BasicStopper(niter=2000))
SLCG.setDefaults(save_obj=True, save_model=True)

Secondly, we run the solvers to minimize the objective functions previously defined.

LCGsolver.run(Phi1, verbose=True)

##########################################################################################
            CG Solver
    Restart folder: /tmp/restart_2022-04-22T01-50-53.913509/
##########################################################################################

iter = 0000, obj = 1.00000e+02, rnorm = 1.41e+01, gnorm = 5.66e+04, feval = 00002
iter = 0001, obj = 9.98000e+01, rnorm = 1.41e+01, gnorm = 4.66e+04, feval = 00004
iter = 0002, obj = 9.96483e+01, rnorm = 1.41e+01, gnorm = 4.20e+04, feval = 00006
iter = 0003, obj = 9.95208e+01, rnorm = 1.41e+01, gnorm = 3.90e+04, feval = 00008
iter = 0004, obj = 9.94086e+01, rnorm = 1.41e+01, gnorm = 3.69e+04, feval = 00010
iter = 0005, obj = 9.93072e+01, rnorm = 1.41e+01, gnorm = 3.52e+04, feval = 00012
iter = 0006, obj = 9.92139e+01, rnorm = 1.41e+01, gnorm = 3.39e+04, feval = 00014
iter = 0007, obj = 9.91271e+01, rnorm = 1.41e+01, gnorm = 3.28e+04, feval = 00016
iter = 0008, obj = 9.90455e+01, rnorm = 1.41e+01, gnorm = 3.18e+04, feval = 00018
iter = 0009, obj = 9.89684e+01, rnorm = 1.41e+01, gnorm = 3.10e+04, feval = 00020
iter = 0010, obj = 9.88950e+01, rnorm = 1.41e+01, gnorm = 3.03e+04, feval = 00022
iter = 0011, obj = 9.88249e+01, rnorm = 1.41e+01, gnorm = 2.96e+04, feval = 00024
iter = 0012, obj = 9.87576e+01, rnorm = 1.41e+01, gnorm = 2.91e+04, feval = 00026
iter = 0013, obj = 9.86929e+01, rnorm = 1.40e+01, gnorm = 2.85e+04, feval = 00028
iter = 0014, obj = 9.86304e+01, rnorm = 1.40e+01, gnorm = 2.80e+04, feval = 00030
iter = 0015, obj = 9.85700e+01, rnorm = 1.40e+01, gnorm = 2.76e+04, feval = 00032
iter = 0016, obj = 9.85114e+01, rnorm = 1.40e+01, gnorm = 2.72e+04, feval = 00034
iter = 0017, obj = 9.84545e+01, rnorm = 1.40e+01, gnorm = 2.68e+04, feval = 00036
iter = 0018, obj = 9.83992e+01, rnorm = 1.40e+01, gnorm = 2.64e+04, feval = 00038
iter = 0019, obj = 9.83453e+01, rnorm = 1.40e+01, gnorm = 2.61e+04, feval = 00040
iter = 0020, obj = 9.82927e+01, rnorm = 1.40e+01, gnorm = 2.58e+04, feval = 00042
iter = 0021, obj = 9.82413e+01, rnorm = 1.40e+01, gnorm = 2.55e+04, feval = 00044
iter = 0022, obj = 9.81911e+01, rnorm = 1.40e+01, gnorm = 2.52e+04, feval = 00046
iter = 0023, obj = 9.81420e+01, rnorm = 1.40e+01, gnorm = 2.49e+04, feval = 00048
iter = 0024, obj = 9.80939e+01, rnorm = 1.40e+01, gnorm = 2.47e+04, feval = 00050
iter = 0025, obj = 9.80468e+01, rnorm = 1.40e+01, gnorm = 2.45e+04, feval = 00052
iter = 0026, obj = 9.80005e+01, rnorm = 1.40e+01, gnorm = 2.42e+04, feval = 00054
iter = 0027, obj = 9.79551e+01, rnorm = 1.40e+01, gnorm = 2.40e+04, feval = 00056
iter = 0028, obj = 9.79104e+01, rnorm = 1.40e+01, gnorm = 2.38e+04, feval = 00058
iter = 0029, obj = 9.78666e+01, rnorm = 1.40e+01, gnorm = 2.36e+04, feval = 00060
iter = 0030, obj = 9.78234e+01, rnorm = 1.40e+01, gnorm = 2.34e+04, feval = 00062
iter = 0031, obj = 9.77810e+01, rnorm = 1.40e+01, gnorm = 2.32e+04, feval = 00064
iter = 0032, obj = 9.77392e+01, rnorm = 1.40e+01, gnorm = 2.30e+04, feval = 00066
iter = 0033, obj = 9.76980e+01, rnorm = 1.40e+01, gnorm = 2.29e+04, feval = 00068
iter = 0034, obj = 9.76575e+01, rnorm = 1.40e+01, gnorm = 2.27e+04, feval = 00070
iter = 0035, obj = 9.76175e+01, rnorm = 1.40e+01, gnorm = 2.25e+04, feval = 00072
iter = 0036, obj = 9.75780e+01, rnorm = 1.40e+01, gnorm = 2.24e+04, feval = 00074
iter = 0037, obj = 9.75391e+01, rnorm = 1.40e+01, gnorm = 2.22e+04, feval = 00076
iter = 0038, obj = 9.75007e+01, rnorm = 1.40e+01, gnorm = 2.21e+04, feval = 00078
iter = 0039, obj = 9.74628e+01, rnorm = 1.40e+01, gnorm = 2.20e+04, feval = 00080
iter = 0040, obj = 9.74253e+01, rnorm = 1.40e+01, gnorm = 2.18e+04, feval = 00082
iter = 0041, obj = 9.73883e+01, rnorm = 1.40e+01, gnorm = 2.17e+04, feval = 00084
iter = 0042, obj = 9.73517e+01, rnorm = 1.40e+01, gnorm = 2.16e+04, feval = 00086
iter = 0043, obj = 9.73156e+01, rnorm = 1.40e+01, gnorm = 2.14e+04, feval = 00088
iter = 0044, obj = 9.72799e+01, rnorm = 1.39e+01, gnorm = 2.13e+04, feval = 00090
iter = 0045, obj = 9.72445e+01, rnorm = 1.39e+01, gnorm = 2.12e+04, feval = 00092
iter = 0046, obj = 9.72096e+01, rnorm = 1.39e+01, gnorm = 2.11e+04, feval = 00094
iter = 0047, obj = 9.71750e+01, rnorm = 1.39e+01, gnorm = 2.10e+04, feval = 00096
iter = 0048, obj = 9.71407e+01, rnorm = 1.39e+01, gnorm = 2.09e+04, feval = 00098
iter = 0049, obj = 9.71068e+01, rnorm = 1.39e+01, gnorm = 2.08e+04, feval = 00100
iter = 0050, obj = 9.70733e+01, rnorm = 1.39e+01, gnorm = 2.07e+04, feval = 00102
iter = 0051, obj = 9.70401e+01, rnorm = 1.39e+01, gnorm = 2.06e+04, feval = 00104
iter = 0052, obj = 9.70071e+01, rnorm = 1.39e+01, gnorm = 2.05e+04, feval = 00106
iter = 0053, obj = 9.69745e+01, rnorm = 1.39e+01, gnorm = 2.04e+04, feval = 00108
iter = 0054, obj = 9.69422e+01, rnorm = 1.39e+01, gnorm = 2.03e+04, feval = 00110
iter = 0055, obj = 9.69102e+01, rnorm = 1.39e+01, gnorm = 2.02e+04, feval = 00112
iter = 0056, obj = 9.68785e+01, rnorm = 1.39e+01, gnorm = 2.01e+04, feval = 00114
iter = 0057, obj = 9.68471e+01, rnorm = 1.39e+01, gnorm = 2.00e+04, feval = 00116
iter = 0058, obj = 9.68159e+01, rnorm = 1.39e+01, gnorm = 1.99e+04, feval = 00118
iter = 0059, obj = 9.67850e+01, rnorm = 1.39e+01, gnorm = 1.99e+04, feval = 00120
iter = 0060, obj = 9.67543e+01, rnorm = 1.39e+01, gnorm = 1.98e+04, feval = 00122
iter = 0061, obj = 9.67239e+01, rnorm = 1.39e+01, gnorm = 1.97e+04, feval = 00124
iter = 0062, obj = 9.66937e+01, rnorm = 1.39e+01, gnorm = 1.96e+04, feval = 00126
iter = 0063, obj = 9.66638e+01, rnorm = 1.39e+01, gnorm = 1.95e+04, feval = 00128
iter = 0064, obj = 9.66341e+01, rnorm = 1.39e+01, gnorm = 1.95e+04, feval = 00130
iter = 0065, obj = 9.66046e+01, rnorm = 1.39e+01, gnorm = 1.94e+04, feval = 00132
iter = 0066, obj = 9.65753e+01, rnorm = 1.39e+01, gnorm = 1.93e+04, feval = 00134
iter = 0067, obj = 9.65463e+01, rnorm = 1.39e+01, gnorm = 1.92e+04, feval = 00136
iter = 0068, obj = 9.65175e+01, rnorm = 1.39e+01, gnorm = 1.92e+04, feval = 00138
iter = 0069, obj = 9.64887e+01, rnorm = 1.39e+01, gnorm = 1.90e+04, feval = 00140
iter = 0070, obj = 9.64595e+01, rnorm = 1.39e+01, gnorm = 1.86e+04, feval = 00142
iter = 0071, obj = 9.64289e+01, rnorm = 1.39e+01, gnorm = 1.78e+04, feval = 00144
iter = 0072, obj = 9.63958e+01, rnorm = 1.39e+01, gnorm = 1.69e+04, feval = 00146
iter = 0073, obj = 9.63594e+01, rnorm = 1.39e+01, gnorm = 1.60e+04, feval = 00148
iter = 0074, obj = 9.63193e+01, rnorm = 1.39e+01, gnorm = 1.51e+04, feval = 00150
iter = 0075, obj = 9.62750e+01, rnorm = 1.39e+01, gnorm = 1.42e+04, feval = 00152
iter = 0076, obj = 9.62261e+01, rnorm = 1.39e+01, gnorm = 1.33e+04, feval = 00154
iter = 0077, obj = 9.61718e+01, rnorm = 1.39e+01, gnorm = 1.25e+04, feval = 00156
iter = 0078, obj = 9.61117e+01, rnorm = 1.39e+01, gnorm = 1.17e+04, feval = 00158
iter = 0079, obj = 9.60451e+01, rnorm = 1.39e+01, gnorm = 1.10e+04, feval = 00160
iter = 0080, obj = 9.59710e+01, rnorm = 1.39e+01, gnorm = 1.02e+04, feval = 00162
iter = 0081, obj = 9.58885e+01, rnorm = 1.38e+01, gnorm = 9.51e+03, feval = 00164
iter = 0082, obj = 9.57994e+01, rnorm = 1.38e+01, gnorm = 1.48e+04, feval = 00166
iter = 0083, obj = 9.57926e+01, rnorm = 1.38e+01, gnorm = 1.07e+04, feval = 00168
iter = 0084, obj = 9.56911e+01, rnorm = 1.38e+01, gnorm = 9.04e+03, feval = 00170
iter = 0085, obj = 9.56825e+01, rnorm = 1.38e+01, gnorm = 1.78e+04, feval = 00172
iter = 0086, obj = 9.55757e+01, rnorm = 1.38e+01, gnorm = 1.31e+04, feval = 00174
iter = 0087, obj = 9.55701e+01, rnorm = 1.38e+01, gnorm = 9.11e+03, feval = 00176
iter = 0088, obj = 9.55005e+01, rnorm = 1.38e+01, gnorm = 3.82e+04, feval = 00178
iter = 0089, obj = 9.54397e+01, rnorm = 1.38e+01, gnorm = 8.27e+03, feval = 00180
iter = 0090, obj = 9.54344e+01, rnorm = 1.38e+01, gnorm = 1.24e+04, feval = 00182
iter = 0091, obj = 9.53471e+01, rnorm = 1.38e+01, gnorm = 3.82e+04, feval = 00184
iter = 0092, obj = 9.52903e+01, rnorm = 1.38e+01, gnorm = 9.52e+03, feval = 00186
iter = 0093, obj = 9.52862e+01, rnorm = 1.38e+01, gnorm = 8.57e+03, feval = 00188
iter = 0094, obj = 9.52539e+01, rnorm = 1.38e+01, gnorm = 3.14e+04, feval = 00190
iter = 0095, obj = 9.51354e+01, rnorm = 1.38e+01, gnorm = 2.39e+04, feval = 00192
iter = 0096, obj = 9.51176e+01, rnorm = 1.38e+01, gnorm = 7.11e+03, feval = 00194
iter = 0097, obj = 9.51134e+01, rnorm = 1.38e+01, gnorm = 1.03e+04, feval = 00196
iter = 0098, obj = 9.50593e+01, rnorm = 1.38e+01, gnorm = 3.70e+04, feval = 00198
iter = 0099, obj = 9.49394e+01, rnorm = 1.38e+01, gnorm = 2.30e+04, feval = 00200
iter = 0100, obj = 9.49226e+01, rnorm = 1.38e+01, gnorm = 7.51e+03, feval = 00202
iter = 0101, obj = 9.49194e+01, rnorm = 1.38e+01, gnorm = 7.56e+03, feval = 00204
iter = 0102, obj = 9.48992e+01, rnorm = 1.38e+01, gnorm = 2.46e+04, feval = 00206
iter = 0103, obj = 9.47920e+01, rnorm = 1.38e+01, gnorm = 4.04e+04, feval = 00208
iter = 0104, obj = 9.47042e+01, rnorm = 1.38e+01, gnorm = 1.53e+04, feval = 00210
iter = 0105, obj = 9.46962e+01, rnorm = 1.38e+01, gnorm = 6.60e+03, feval = 00212
iter = 0106, obj = 9.46933e+01, rnorm = 1.38e+01, gnorm = 7.43e+03, feval = 00214
iter = 0107, obj = 9.46815e+01, rnorm = 1.38e+01, gnorm = 1.84e+04, feval = 00216
iter = 0108, obj = 9.45974e+01, rnorm = 1.38e+01, gnorm = 4.02e+04, feval = 00218
iter = 0109, obj = 9.44682e+01, rnorm = 1.37e+01, gnorm = 2.83e+04, feval = 00220
iter = 0110, obj = 9.44356e+01, rnorm = 1.37e+01, gnorm = 9.94e+03, feval = 00222
iter = 0111, obj = 9.44317e+01, rnorm = 1.37e+01, gnorm = 5.75e+03, feval = 00224
iter = 0112, obj = 9.44286e+01, rnorm = 1.37e+01, gnorm = 7.69e+03, feval = 00226
iter = 0113, obj = 9.44184e+01, rnorm = 1.37e+01, gnorm = 1.61e+04, feval = 00228
iter = 0114, obj = 9.43520e+01, rnorm = 1.37e+01, gnorm = 3.91e+04, feval = 00230
iter = 0115, obj = 9.41911e+01, rnorm = 1.37e+01, gnorm = 3.70e+04, feval = 00232
iter = 0116, obj = 9.41331e+01, rnorm = 1.37e+01, gnorm = 1.62e+04, feval = 00234
iter = 0117, obj = 9.41219e+01, rnorm = 1.37e+01, gnorm = 7.76e+03, feval = 00236
iter = 0118, obj = 9.41190e+01, rnorm = 1.37e+01, gnorm = 5.04e+03, feval = 00238
iter = 0119, obj = 9.41165e+01, rnorm = 1.37e+01, gnorm = 7.51e+03, feval = 00240
iter = 0120, obj = 9.41064e+01, rnorm = 1.37e+01, gnorm = 1.61e+04, feval = 00242

iter = 0121, obj = 9.40543e+01, rnorm = 1.37e+01, gnorm = 3.20e+04, feval = 00244
iter = 0122, obj = 9.39411e+01, rnorm = 1.37e+01, gnorm = 4.37e+04, feval = 00246
iter = 0123, obj = 9.37967e+01, rnorm = 1.37e+01, gnorm = 3.13e+04, feval = 00248
iter = 0124, obj = 9.37544e+01, rnorm = 1.37e+01, gnorm = 1.42e+04, feval = 00250
iter = 0125, obj = 9.37464e+01, rnorm = 1.37e+01, gnorm = 7.09e+03, feval = 00252
iter = 0126, obj = 9.37437e+01, rnorm = 1.37e+01, gnorm = 4.84e+03, feval = 00254
iter = 0127, obj = 9.37419e+01, rnorm = 1.37e+01, gnorm = 5.55e+03, feval = 00256
iter = 0128, obj = 9.37376e+01, rnorm = 1.37e+01, gnorm = 1.04e+04, feval = 00258
iter = 0129, obj = 9.37140e+01, rnorm = 1.37e+01, gnorm = 2.07e+04, feval = 00260
iter = 0130, obj = 9.36340e+01, rnorm = 1.37e+01, gnorm = 3.98e+04, feval = 00262
iter = 0131, obj = 9.34869e+01, rnorm = 1.37e+01, gnorm = 4.41e+04, feval = 00264
iter = 0132, obj = 9.33549e+01, rnorm = 1.37e+01, gnorm = 3.36e+04, feval = 00266
iter = 0133, obj = 9.32981e+01, rnorm = 1.37e+01, gnorm = 1.74e+04, feval = 00268
iter = 0134, obj = 9.32866e+01, rnorm = 1.37e+01, gnorm = 7.56e+03, feval = 00270
iter = 0135, obj = 9.32833e+01, rnorm = 1.37e+01, gnorm = 5.67e+03, feval = 00272
iter = 0136, obj = 9.32815e+01, rnorm = 1.37e+01, gnorm = 4.49e+03, feval = 00274
iter = 0137, obj = 9.32798e+01, rnorm = 1.37e+01, gnorm = 5.42e+03, feval = 00276
iter = 0138, obj = 9.32762e+01, rnorm = 1.37e+01, gnorm = 7.43e+03, feval = 00278
iter = 0139, obj = 9.32671e+01, rnorm = 1.37e+01, gnorm = 1.45e+04, feval = 00280
iter = 0140, obj = 9.32352e+01, rnorm = 1.37e+01, gnorm = 2.58e+04, feval = 00282
iter = 0141, obj = 9.31132e+01, rnorm = 1.36e+01, gnorm = 4.32e+04, feval = 00284
iter = 0142, obj = 9.28735e+01, rnorm = 1.36e+01, gnorm = 3.78e+04, feval = 00286
iter = 0143, obj = 9.27669e+01, rnorm = 1.36e+01, gnorm = 2.95e+04, feval = 00288
iter = 0144, obj = 9.27118e+01, rnorm = 1.36e+01, gnorm = 1.37e+04, feval = 00290
iter = 0145, obj = 9.27027e+01, rnorm = 1.36e+01, gnorm = 7.51e+03, feval = 00292
iter = 0146, obj = 9.26985e+01, rnorm = 1.36e+01, gnorm = 3.74e+03, feval = 00294
iter = 0147, obj = 9.26961e+01, rnorm = 1.36e+01, gnorm = 3.29e+03, feval = 00296
iter = 0148, obj = 9.26935e+01, rnorm = 1.36e+01, gnorm = 5.01e+03, feval = 00298
iter = 0149, obj = 9.26860e+01, rnorm = 1.36e+01, gnorm = 9.65e+03, feval = 00300
iter = 0150, obj = 9.26522e+01, rnorm = 1.36e+01, gnorm = 1.73e+04, feval = 00302
iter = 0151, obj = 9.24926e+01, rnorm = 1.36e+01, gnorm = 3.42e+04, feval = 00304
iter = 0152, obj = 9.22854e+01, rnorm = 1.36e+01, gnorm = 3.01e+04, feval = 00306
iter = 0153, obj = 9.21362e+01, rnorm = 1.36e+01, gnorm = 3.20e+04, feval = 00308
iter = 0154, obj = 9.19493e+01, rnorm = 1.36e+01, gnorm = 1.19e+04, feval = 00310
iter = 0155, obj = 9.19361e+01, rnorm = 1.36e+01, gnorm = 1.23e+04, feval = 00312
iter = 0156, obj = 9.19314e+01, rnorm = 1.36e+01, gnorm = 4.70e+03, feval = 00314
iter = 0157, obj = 9.19266e+01, rnorm = 1.36e+01, gnorm = 2.37e+03, feval = 00316
iter = 0158, obj = 9.19243e+01, rnorm = 1.36e+01, gnorm = 5.13e+03, feval = 00318
iter = 0159, obj = 9.19233e+01, rnorm = 1.36e+01, gnorm = 3.65e+03, feval = 00320
iter = 0160, obj = 9.19181e+01, rnorm = 1.36e+01, gnorm = 4.92e+03, feval = 00322
iter = 0161, obj = 9.19036e+01, rnorm = 1.36e+01, gnorm = 2.24e+04, feval = 00324
iter = 0162, obj = 9.18569e+01, rnorm = 1.36e+01, gnorm = 1.87e+04, feval = 00326
iter = 0163, obj = 9.16903e+01, rnorm = 1.35e+01, gnorm = 5.44e+04, feval = 00328
iter = 0164, obj = 9.15757e+01, rnorm = 1.35e+01, gnorm = 2.71e+04, feval = 00330
iter = 0165, obj = 9.12069e+01, rnorm = 1.35e+01, gnorm = 7.56e+04, feval = 00332
iter = 0166, obj = 9.10037e+01, rnorm = 1.35e+01, gnorm = 2.07e+04, feval = 00334
iter = 0167, obj = 9.09239e+01, rnorm = 1.35e+01, gnorm = 3.74e+04, feval = 00336
iter = 0168, obj = 9.08715e+01, rnorm = 1.35e+01, gnorm = 8.63e+03, feval = 00338
iter = 0169, obj = 9.08660e+01, rnorm = 1.35e+01, gnorm = 1.04e+04, feval = 00340
iter = 0170, obj = 9.08569e+01, rnorm = 1.35e+01, gnorm = 4.40e+03, feval = 00342
iter = 0171, obj = 9.08562e+01, rnorm = 1.35e+01, gnorm = 3.63e+03, feval = 00344
iter = 0172, obj = 9.08536e+01, rnorm = 1.35e+01, gnorm = 4.09e+03, feval = 00346
iter = 0173, obj = 9.08531e+01, rnorm = 1.35e+01, gnorm = 1.89e+03, feval = 00348
iter = 0174, obj = 9.08526e+01, rnorm = 1.35e+01, gnorm = 3.72e+03, feval = 00350
iter = 0175, obj = 9.08506e+01, rnorm = 1.35e+01, gnorm = 3.40e+03, feval = 00352
iter = 0176, obj = 9.08498e+01, rnorm = 1.35e+01, gnorm = 4.65e+03, feval = 00354
iter = 0177, obj = 9.08413e+01, rnorm = 1.35e+01, gnorm = 1.20e+04, feval = 00356
iter = 0178, obj = 9.08339e+01, rnorm = 1.35e+01, gnorm = 7.66e+03, feval = 00358
iter = 0179, obj = 9.08272e+01, rnorm = 1.35e+01, gnorm = 1.37e+04, feval = 00360
iter = 0180, obj = 9.07326e+01, rnorm = 1.35e+01, gnorm = 4.30e+04, feval = 00362
iter = 0181, obj = 9.06355e+01, rnorm = 1.35e+01, gnorm = 2.36e+04, feval = 00364
iter = 0182, obj = 9.05784e+01, rnorm = 1.35e+01, gnorm = 4.08e+04, feval = 00366
iter = 0183, obj = 9.00352e+01, rnorm = 1.34e+01, gnorm = 8.76e+04, feval = 00368
iter = 0184, obj = 8.97072e+01, rnorm = 1.34e+01, gnorm = 3.45e+04, feval = 00370
iter = 0185, obj = 8.96426e+01, rnorm = 1.34e+01, gnorm = 3.18e+04, feval = 00372
iter = 0186, obj = 8.94410e+01, rnorm = 1.34e+01, gnorm = 6.11e+04, feval = 00374
iter = 0187, obj = 8.92568e+01, rnorm = 1.34e+01, gnorm = 1.88e+04, feval = 00376
iter = 0188, obj = 8.92460e+01, rnorm = 1.34e+01, gnorm = 7.08e+03, feval = 00378
iter = 0189, obj = 8.92411e+01, rnorm = 1.34e+01, gnorm = 1.07e+04, feval = 00380
iter = 0190, obj = 8.92277e+01, rnorm = 1.34e+01, gnorm = 8.71e+03, feval = 00382
iter = 0191, obj = 8.92245e+01, rnorm = 1.34e+01, gnorm = 3.72e+03, feval = 00384
iter = 0192, obj = 8.92237e+01, rnorm = 1.34e+01, gnorm = 3.41e+03, feval = 00386
iter = 0193, obj = 8.92222e+01, rnorm = 1.34e+01, gnorm = 4.01e+03, feval = 00388
iter = 0194, obj = 8.92215e+01, rnorm = 1.34e+01, gnorm = 1.68e+03, feval = 00390
iter = 0195, obj = 8.92214e+01, rnorm = 1.34e+01, gnorm = 1.43e+03, feval = 00392
iter = 0196, obj = 8.92209e+01, rnorm = 1.34e+01, gnorm = 3.37e+03, feval = 00394
iter = 0197, obj = 8.92193e+01, rnorm = 1.34e+01, gnorm = 4.12e+03, feval = 00396
iter = 0198, obj = 8.92186e+01, rnorm = 1.34e+01, gnorm = 1.97e+03, feval = 00398
iter = 0199, obj = 8.92182e+01, rnorm = 1.34e+01, gnorm = 3.12e+03, feval = 00400
iter = 0200, obj = 8.92128e+01, rnorm = 1.34e+01, gnorm = 1.29e+04, feval = 00402
iter = 0201, obj = 8.91858e+01, rnorm = 1.34e+01, gnorm = 1.81e+04, feval = 00404
iter = 0202, obj = 8.91645e+01, rnorm = 1.34e+01, gnorm = 1.32e+04, feval = 00406
iter = 0203, obj = 8.91540e+01, rnorm = 1.34e+01, gnorm = 1.09e+04, feval = 00408
iter = 0204, obj = 8.91370e+01, rnorm = 1.34e+01, gnorm = 2.07e+04, feval = 00410
iter = 0205, obj = 8.89646e+01, rnorm = 1.33e+01, gnorm = 6.17e+04, feval = 00412
iter = 0206, obj = 8.84547e+01, rnorm = 1.33e+01, gnorm = 8.97e+04, feval = 00414
iter = 0207, obj = 8.80282e+01, rnorm = 1.33e+01, gnorm = 4.73e+04, feval = 00416
iter = 0208, obj = 8.79071e+01, rnorm = 1.33e+01, gnorm = 3.53e+04, feval = 00418
iter = 0209, obj = 8.77829e+01, rnorm = 1.33e+01, gnorm = 5.18e+04, feval = 00420
iter = 0210, obj = 8.73399e+01, rnorm = 1.32e+01, gnorm = 9.03e+04, feval = 00422
iter = 0211, obj = 8.66031e+01, rnorm = 1.32e+01, gnorm = 6.73e+04, feval = 00424
iter = 0212, obj = 8.63922e+01, rnorm = 1.31e+01, gnorm = 2.46e+04, feval = 00426
iter = 0213, obj = 8.63691e+01, rnorm = 1.31e+01, gnorm = 9.95e+03, feval = 00428
iter = 0214, obj = 8.63630e+01, rnorm = 1.31e+01, gnorm = 8.55e+03, feval = 00430
iter = 0215, obj = 8.63474e+01, rnorm = 1.31e+01, gnorm = 1.51e+04, feval = 00432
iter = 0216, obj = 8.63192e+01, rnorm = 1.31e+01, gnorm = 9.48e+03, feval = 00434
iter = 0217, obj = 8.63154e+01, rnorm = 1.31e+01, gnorm = 2.92e+03, feval = 00436
iter = 0218, obj = 8.63150e+01, rnorm = 1.31e+01, gnorm = 1.60e+03, feval = 00438
iter = 0219, obj = 8.63148e+01, rnorm = 1.31e+01, gnorm = 1.65e+03, feval = 00440
iter = 0220, obj = 8.63142e+01, rnorm = 1.31e+01, gnorm = 2.54e+03, feval = 00442
iter = 0221, obj = 8.63130e+01, rnorm = 1.31e+01, gnorm = 2.45e+03, feval = 00444
iter = 0222, obj = 8.63126e+01, rnorm = 1.31e+01, gnorm = 7.21e+02, feval = 00446
iter = 0223, obj = 8.63126e+01, rnorm = 1.31e+01, gnorm = 8.32e+02, feval = 00448
iter = 0224, obj = 8.63119e+01, rnorm = 1.31e+01, gnorm = 2.69e+03, feval = 00450
iter = 0225, obj = 8.63099e+01, rnorm = 1.31e+01, gnorm = 3.75e+03, feval = 00452
iter = 0226, obj = 8.63090e+01, rnorm = 1.31e+01, gnorm = 3.06e+03, feval = 00454
iter = 0227, obj = 8.63087e+01, rnorm = 1.31e+01, gnorm = 1.72e+03, feval = 00456
iter = 0228, obj = 8.63080e+01, rnorm = 1.31e+01, gnorm = 2.72e+03, feval = 00458
iter = 0229, obj = 8.62963e+01, rnorm = 1.31e+01, gnorm = 1.15e+04, feval = 00460
iter = 0230, obj = 8.62444e+01, rnorm = 1.31e+01, gnorm = 4.46e+04, feval = 00462
iter = 0231, obj = 8.59920e+01, rnorm = 1.31e+01, gnorm = 4.85e+04, feval = 00464
iter = 0232, obj = 8.56478e+01, rnorm = 1.31e+01, gnorm = 2.82e+04, feval = 00466
iter = 0233, obj = 8.55580e+01, rnorm = 1.31e+01, gnorm = 1.86e+04, feval = 00468
iter = 0234, obj = 8.53869e+01, rnorm = 1.31e+01, gnorm = 8.20e+04, feval = 00470
iter = 0235, obj = 8.44416e+01, rnorm = 1.30e+01, gnorm = 8.75e+04, feval = 00472
iter = 0236, obj = 8.26137e+01, rnorm = 1.29e+01, gnorm = 1.14e+05, feval = 00474
iter = 0237, obj = 8.22005e+01, rnorm = 1.28e+01, gnorm = 6.06e+04, feval = 00476
iter = 0238, obj = 8.18526e+01, rnorm = 1.28e+01, gnorm = 4.37e+04, feval = 00478
iter = 0239, obj = 8.16727e+01, rnorm = 1.28e+01, gnorm = 5.17e+04, feval = 00480
iter = 0240, obj = 8.15321e+01, rnorm = 1.28e+01, gnorm = 4.87e+04, feval = 00482
iter = 0241, obj = 8.03312e+01, rnorm = 1.27e+01, gnorm = 9.98e+04, feval = 00484
iter = 0242, obj = 7.97336e+01, rnorm = 1.26e+01, gnorm = 1.05e+05, feval = 00486
iter = 0243, obj = 7.90122e+01, rnorm = 1.26e+01, gnorm = 2.74e+04, feval = 00488
iter = 0244, obj = 7.89756e+01, rnorm = 1.26e+01, gnorm = 2.54e+04, feval = 00490
iter = 0245, obj = 7.89336e+01, rnorm = 1.26e+01, gnorm = 6.04e+03, feval = 00492
iter = 0246, obj = 7.89326e+01, rnorm = 1.26e+01, gnorm = 3.09e+03, feval = 00494
iter = 0247, obj = 7.89316e+01, rnorm = 1.26e+01, gnorm = 2.29e+03, feval = 00496
iter = 0248, obj = 7.89314e+01, rnorm = 1.26e+01, gnorm = 1.27e+03, feval = 00498
iter = 0249, obj = 7.89308e+01, rnorm = 1.26e+01, gnorm = 4.13e+03, feval = 00500
iter = 0250, obj = 7.89295e+01, rnorm = 1.26e+01, gnorm = 2.83e+03, feval = 00502
iter = 0251, obj = 7.89281e+01, rnorm = 1.26e+01, gnorm = 4.32e+03, feval = 00504
iter = 0252, obj = 7.89274e+01, rnorm = 1.26e+01, gnorm = 1.59e+03, feval = 00506
iter = 0253, obj = 7.89272e+01, rnorm = 1.26e+01, gnorm = 1.86e+03, feval = 00508
iter = 0254, obj = 7.89269e+01, rnorm = 1.26e+01, gnorm = 8.07e+02, feval = 00510
iter = 0255, obj = 7.89269e+01, rnorm = 1.26e+01, gnorm = 4.22e+02, feval = 00512
iter = 0256, obj = 7.89268e+01, rnorm = 1.26e+01, gnorm = 1.37e+03, feval = 00514
iter = 0257, obj = 7.89267e+01, rnorm = 1.26e+01, gnorm = 1.03e+03, feval = 00516
iter = 0258, obj = 7.89266e+01, rnorm = 1.26e+01, gnorm = 1.56e+03, feval = 00518
iter = 0259, obj = 7.89264e+01, rnorm = 1.26e+01, gnorm = 6.97e+02, feval = 00520
iter = 0260, obj = 7.89264e+01, rnorm = 1.26e+01, gnorm = 2.68e+02, feval = 00522
iter = 0261, obj = 7.89264e+01, rnorm = 1.26e+01, gnorm = 4.18e+02, feval = 00524
iter = 0262, obj = 7.89264e+01, rnorm = 1.26e+01, gnorm = 2.58e+02, feval = 00526
iter = 0263, obj = 7.89264e+01, rnorm = 1.26e+01, gnorm = 3.54e+02, feval = 00528
iter = 0264, obj = 7.89262e+01, rnorm = 1.26e+01, gnorm = 1.99e+03, feval = 00530
iter = 0265, obj = 7.89257e+01, rnorm = 1.26e+01, gnorm = 1.94e+03, feval = 00532
iter = 0266, obj = 7.89254e+01, rnorm = 1.26e+01, gnorm = 2.87e+03, feval = 00534
iter = 0267, obj = 7.89233e+01, rnorm = 1.26e+01, gnorm = 5.85e+03, feval = 00536
iter = 0268, obj = 7.89216e+01, rnorm = 1.26e+01, gnorm = 3.66e+03, feval = 00538
iter = 0269, obj = 7.89199e+01, rnorm = 1.26e+01, gnorm = 5.88e+03, feval = 00540
iter = 0270, obj = 7.89165e+01, rnorm = 1.26e+01, gnorm = 5.02e+03, feval = 00542
iter = 0271, obj = 7.89156e+01, rnorm = 1.26e+01, gnorm = 1.96e+03, feval = 00544
iter = 0272, obj = 7.89151e+01, rnorm = 1.26e+01, gnorm = 3.58e+03, feval = 00546
iter = 0273, obj = 7.89135e+01, rnorm = 1.26e+01, gnorm = 3.53e+03, feval = 00548
iter = 0274, obj = 7.89125e+01, rnorm = 1.26e+01, gnorm = 4.32e+03, feval = 00550
iter = 0275, obj = 7.89084e+01, rnorm = 1.26e+01, gnorm = 1.02e+04, feval = 00552
iter = 0276, obj = 7.88913e+01, rnorm = 1.26e+01, gnorm = 1.21e+04, feval = 00554
iter = 0277, obj = 7.88823e+01, rnorm = 1.26e+01, gnorm = 1.04e+04, feval = 00556
iter = 0278, obj = 7.88650e+01, rnorm = 1.26e+01, gnorm = 2.10e+04, feval = 00558
iter = 0279, obj = 7.88125e+01, rnorm = 1.26e+01, gnorm = 2.25e+04, feval = 00560
iter = 0280, obj = 7.87930e+01, rnorm = 1.26e+01, gnorm = 7.36e+03, feval = 00562
iter = 0281, obj = 7.87882e+01, rnorm = 1.26e+01, gnorm = 1.05e+04, feval = 00564
iter = 0282, obj = 7.87724e+01, rnorm = 1.26e+01, gnorm = 1.41e+04, feval = 00566
iter = 0283, obj = 7.87614e+01, rnorm = 1.26e+01, gnorm = 7.84e+03, feval = 00568
iter = 0284, obj = 7.87493e+01, rnorm = 1.25e+01, gnorm = 1.76e+04, feval = 00570
iter = 0285, obj = 7.85940e+01, rnorm = 1.25e+01, gnorm = 4.43e+04, feval = 00572
iter = 0286, obj = 7.84559e+01, rnorm = 1.25e+01, gnorm = 3.42e+04, feval = 00574
iter = 0287, obj = 7.82204e+01, rnorm = 1.25e+01, gnorm = 7.84e+04, feval = 00576
iter = 0288, obj = 7.63551e+01, rnorm = 1.24e+01, gnorm = 1.65e+05, feval = 00578
iter = 0289, obj = 7.46982e+01, rnorm = 1.22e+01, gnorm = 8.06e+04, feval = 00580
iter = 0290, obj = 7.38587e+01, rnorm = 1.22e+01, gnorm = 9.97e+04, feval = 00582
iter = 0291, obj = 7.20386e+01, rnorm = 1.20e+01, gnorm = 9.76e+04, feval = 00584
iter = 0292, obj = 7.14985e+01, rnorm = 1.20e+01, gnorm = 4.01e+04, feval = 00586
iter = 0293, obj = 7.12858e+01, rnorm = 1.19e+01, gnorm = 6.56e+04, feval = 00588
iter = 0294, obj = 7.05149e+01, rnorm = 1.19e+01, gnorm = 1.12e+05, feval = 00590
iter = 0295, obj = 6.84456e+01, rnorm = 1.17e+01, gnorm = 1.05e+05, feval = 00592
iter = 0296, obj = 6.73479e+01, rnorm = 1.16e+01, gnorm = 1.53e+05, feval = 00594
iter = 0297, obj = 6.39557e+01, rnorm = 1.13e+01, gnorm = 3.13e+05, feval = 00596

iter = 0298, obj = 4.98865e+01, rnorm = 9.99e+00, gnorm = 4.18e+05, feval = 00598
iter = 0299, obj = 3.35917e+01, rnorm = 8.20e+00, gnorm = 2.33e+05, feval = 00600
iter = 0300, obj = 1.97988e+01, rnorm = 6.29e+00, gnorm = 3.08e+05, feval = 00602
iter = 0301, obj = 9.29499e+00, rnorm = 4.31e+00, gnorm = 2.08e+05, feval = 00604
iter = 0302, obj = 7.40993e+00, rnorm = 3.85e+00, gnorm = 1.18e+05, feval = 00606
iter = 0303, obj = 6.99169e+00, rnorm = 3.74e+00, gnorm = 4.24e+04, feval = 00608
iter = 0304, obj = 6.12529e+00, rnorm = 3.50e+00, gnorm = 6.53e+04, feval = 00610
iter = 0305, obj = 5.84772e+00, rnorm = 3.42e+00, gnorm = 2.88e+04, feval = 00612
iter = 0306, obj = 5.73638e+00, rnorm = 3.39e+00, gnorm = 5.93e+04, feval = 00614
iter = 0307, obj = 5.32788e+00, rnorm = 3.26e+00, gnorm = 8.54e+04, feval = 00616
iter = 0308, obj = 2.75342e-01, rnorm = 7.42e-01, gnorm = 5.77e+04, feval = 00618
iter = 0309, obj = 1.46648e-01, rnorm = 5.42e-01, gnorm = 3.66e+04, feval = 00620
iter = 0310, obj = 9.50978e-02, rnorm = 4.36e-01, gnorm = 1.23e+04, feval = 00622
iter = 0311, obj = 7.03705e-02, rnorm = 3.75e-01, gnorm = 1.49e+04, feval = 00624
iter = 0312, obj = 5.82868e-02, rnorm = 3.41e-01, gnorm = 1.59e+04, feval = 00626
iter = 0313, obj = 3.13612e-02, rnorm = 2.50e-01, gnorm = 4.86e+03, feval = 00628
iter = 0314, obj = 3.01569e-02, rnorm = 2.46e-01, gnorm = 3.67e+03, feval = 00630
iter = 0315, obj = 2.96609e-02, rnorm = 2.44e-01, gnorm = 1.59e+03, feval = 00632
iter = 0316, obj = 2.89121e-02, rnorm = 2.40e-01, gnorm = 3.36e+03, feval = 00634
iter = 0317, obj = 2.80082e-02, rnorm = 2.37e-01, gnorm = 4.75e+03, feval = 00636
iter = 0318, obj = 2.40827e-02, rnorm = 2.19e-01, gnorm = 3.89e+03, feval = 00638
iter = 0319, obj = 2.29647e-02, rnorm = 2.14e-01, gnorm = 4.47e+03, feval = 00640
iter = 0320, obj = 2.17708e-02, rnorm = 2.09e-01, gnorm = 3.47e+03, feval = 00642
iter = 0321, obj = 1.47556e-02, rnorm = 1.72e-01, gnorm = 1.32e+04, feval = 00644
iter = 0322, obj = 5.28578e-03, rnorm = 1.03e-01, gnorm = 6.27e+03, feval = 00646
iter = 0323, obj = 1.93650e-03, rnorm = 6.22e-02, gnorm = 4.17e+03, feval = 00648
iter = 0324, obj = 1.48571e-03, rnorm = 5.45e-02, gnorm = 1.05e+03, feval = 00650
iter = 0325, obj = 1.32329e-03, rnorm = 5.14e-02, gnorm = 1.62e+03, feval = 00652
iter = 0326, obj = 1.17840e-03, rnorm = 4.85e-02, gnorm = 1.34e+03, feval = 00654
iter = 0327, obj = 9.29601e-04, rnorm = 4.31e-02, gnorm = 1.36e+03, feval = 00656
iter = 0328, obj = 8.64856e-04, rnorm = 4.16e-02, gnorm = 5.27e+02, feval = 00658
iter = 0329, obj = 8.50669e-04, rnorm = 4.12e-02, gnorm = 2.93e+02, feval = 00660
iter = 0330, obj = 8.44711e-04, rnorm = 4.11e-02, gnorm = 3.59e+02, feval = 00662
iter = 0331, obj = 8.04424e-04, rnorm = 4.01e-02, gnorm = 7.73e+02, feval = 00664
iter = 0332, obj = 7.47683e-04, rnorm = 3.87e-02, gnorm = 1.12e+03, feval = 00666
iter = 0333, obj = 4.56847e-04, rnorm = 3.02e-02, gnorm = 1.93e+03, feval = 00668
iter = 0334, obj = 3.16368e-04, rnorm = 2.52e-02, gnorm = 8.38e+02, feval = 00670
iter = 0335, obj = 2.49844e-04, rnorm = 2.24e-02, gnorm = 7.59e+02, feval = 00672
iter = 0336, obj = 2.21775e-04, rnorm = 2.11e-02, gnorm = 5.80e+02, feval = 00674
iter = 0337, obj = 1.64330e-04, rnorm = 1.81e-02, gnorm = 1.22e+03, feval = 00676
iter = 0338, obj = 3.28861e-05, rnorm = 8.11e-03, gnorm = 5.60e+02, feval = 00678
iter = 0339, obj = 2.14097e-05, rnorm = 6.54e-03, gnorm = 3.63e+02, feval = 00680
iter = 0340, obj = 1.11507e-05, rnorm = 4.72e-03, gnorm = 1.29e+02, feval = 00682
iter = 0341, obj = 1.06153e-05, rnorm = 4.61e-03, gnorm = 4.45e+01, feval = 00684
iter = 0342, obj = 1.04430e-05, rnorm = 4.57e-03, gnorm = 5.59e+01, feval = 00686
iter = 0343, obj = 1.01959e-05, rnorm = 4.52e-03, gnorm = 4.29e+01, feval = 00688
iter = 0344, obj = 1.00086e-05, rnorm = 4.47e-03, gnorm = 6.74e+01, feval = 00690
iter = 0345, obj = 9.19456e-06, rnorm = 4.29e-03, gnorm = 7.06e+01, feval = 00692
iter = 0346, obj = 9.00833e-06, rnorm = 4.24e-03, gnorm = 2.88e+01, feval = 00694
iter = 0347, obj = 8.87419e-06, rnorm = 4.21e-03, gnorm = 4.56e+01, feval = 00696
iter = 0348, obj = 8.75230e-06, rnorm = 4.18e-03, gnorm = 3.58e+01, feval = 00698
iter = 0349, obj = 8.08523e-06, rnorm = 4.02e-03, gnorm = 1.62e+02, feval = 00700
iter = 0350, obj = 2.90767e-06, rnorm = 2.41e-03, gnorm = 1.49e+02, feval = 00702
iter = 0351, obj = 2.13994e-06, rnorm = 2.07e-03, gnorm = 5.81e+01, feval = 00704
iter = 0352, obj = 1.86481e-06, rnorm = 1.93e-03, gnorm = 6.56e+01, feval = 00706
iter = 0353, obj = 1.38554e-06, rnorm = 1.66e-03, gnorm = 5.93e+01, feval = 00708
iter = 0354, obj = 1.17868e-06, rnorm = 1.54e-03, gnorm = 5.68e+01, feval = 00710
iter = 0355, obj = 5.12514e-07, rnorm = 1.01e-03, gnorm = 9.65e+01, feval = 00712
iter = 0356, obj = 1.06203e-07, rnorm = 4.61e-04, gnorm = 2.62e+01, feval = 00714
iter = 0357, obj = 5.53705e-08, rnorm = 3.33e-04, gnorm = 1.92e+01, feval = 00716
iter = 0358, obj = 2.64433e-08, rnorm = 2.30e-04, gnorm = 5.93e+00, feval = 00718
iter = 0359, obj = 2.44984e-08, rnorm = 2.21e-04, gnorm = 3.56e+00, feval = 00720
iter = 0360, obj = 2.24334e-08, rnorm = 2.12e-04, gnorm = 6.35e+00, feval = 00722
iter = 0361, obj = 1.93468e-08, rnorm = 1.97e-04, gnorm = 4.16e+00, feval = 00724
iter = 0362, obj = 1.79202e-08, rnorm = 1.89e-04, gnorm = 4.39e+00, feval = 00726
iter = 0363, obj = 1.43709e-08, rnorm = 1.70e-04, gnorm = 3.19e+00, feval = 00728
iter = 0364, obj = 1.39977e-08, rnorm = 1.67e-04, gnorm = 1.12e+00, feval = 00730
iter = 0365, obj = 1.39388e-08, rnorm = 1.67e-04, gnorm = 1.09e+00, feval = 00732
iter = 0366, obj = 1.38076e-08, rnorm = 1.66e-04, gnorm = 8.38e-01, feval = 00734
iter = 0367, obj = 1.37591e-08, rnorm = 1.66e-04, gnorm = 8.76e-01, feval = 00736
iter = 0368, obj = 1.34702e-08, rnorm = 1.64e-04, gnorm = 2.65e+00, feval = 00738
iter = 0369, obj = 1.07050e-08, rnorm = 1.46e-04, gnorm = 4.03e+00, feval = 00740
iter = 0370, obj = 8.79042e-09, rnorm = 1.33e-04, gnorm = 5.87e+00, feval = 00742
iter = 0371, obj = 3.70225e-09, rnorm = 8.60e-05, gnorm = 8.41e+00, feval = 00744
iter = 0372, obj = 1.17343e-09, rnorm = 4.84e-05, gnorm = 2.29e+00, feval = 00746
iter = 0373, obj = 1.02173e-09, rnorm = 4.52e-05, gnorm = 7.19e-01, feval = 00748
iter = 0374, obj = 9.27027e-10, rnorm = 4.31e-05, gnorm = 1.01e+00, feval = 00750
iter = 0375, obj = 7.81920e-10, rnorm = 3.95e-05, gnorm = 1.02e+00, feval = 00752
iter = 0376, obj = 6.92414e-10, rnorm = 3.72e-05, gnorm = 1.21e+00, feval = 00754
iter = 0377, obj = 5.22944e-10, rnorm = 3.23e-05, gnorm = 1.91e+00, feval = 00756
iter = 0378, obj = 3.33336e-10, rnorm = 2.58e-05, gnorm = 5.44e-01, feval = 00758
iter = 0379, obj = 3.16895e-10, rnorm = 2.52e-05, gnorm = 8.58e-02, feval = 00760
iter = 0380, obj = 3.16093e-10, rnorm = 2.51e-05, gnorm = 9.12e-02, feval = 00762
iter = 0381, obj = 3.14535e-10, rnorm = 2.51e-05, gnorm = 2.36e-01, feval = 00764
iter = 0382, obj = 3.06968e-10, rnorm = 2.48e-05, gnorm = 2.04e-01, feval = 00766
iter = 0383, obj = 3.01151e-10, rnorm = 2.45e-05, gnorm = 3.09e-01, feval = 00768
iter = 0384, obj = 2.80177e-10, rnorm = 2.37e-05, gnorm = 8.89e-01, feval = 00770
iter = 0385, obj = 9.24071e-11, rnorm = 1.36e-05, gnorm = 5.19e-01, feval = 00772
iter = 0386, obj = 6.52657e-11, rnorm = 1.14e-05, gnorm = 7.56e-01, feval = 00774
iter = 0387, obj = 3.22234e-11, rnorm = 8.03e-06, gnorm = 5.42e-01, feval = 00776
iter = 0388, obj = 1.07378e-11, rnorm = 4.63e-06, gnorm = 2.72e-01, feval = 00778
iter = 0389, obj = 6.21057e-12, rnorm = 3.52e-06, gnorm = 1.08e-01, feval = 00780
iter = 0390, obj = 5.80519e-12, rnorm = 3.41e-06, gnorm = 8.17e-02, feval = 00782
iter = 0391, obj = 3.70255e-12, rnorm = 2.72e-06, gnorm = 8.16e-02, feval = 00784
iter = 0392, obj = 3.41827e-12, rnorm = 2.61e-06, gnorm = 7.24e-02, feval = 00786
iter = 0393, obj = 2.61143e-12, rnorm = 2.29e-06, gnorm = 9.37e-02, feval = 00788
iter = 0394, obj = 1.37797e-12, rnorm = 1.66e-06, gnorm = 1.23e-01, feval = 00790
iter = 0395, obj = 8.87239e-13, rnorm = 1.33e-06, gnorm = 3.43e-02, feval = 00792
iter = 0396, obj = 7.54208e-13, rnorm = 1.23e-06, gnorm = 4.13e-02, feval = 00794
iter = 0397, obj = 6.58235e-13, rnorm = 1.15e-06, gnorm = 3.64e-02, feval = 00796
iter = 0398, obj = 5.40312e-13, rnorm = 1.04e-06, gnorm = 1.08e-02, feval = 00798
iter = 0399, obj = 5.33993e-13, rnorm = 1.03e-06, gnorm = 1.29e-02, feval = 00800
iter = 0400, obj = 4.65828e-13, rnorm = 9.65e-07, gnorm = 1.89e-02, feval = 00802
iter = 0401, obj = 4.50120e-13, rnorm = 9.49e-07, gnorm = 1.53e-02, feval = 00804
iter = 0402, obj = 4.27915e-13, rnorm = 9.25e-07, gnorm = 1.39e-02, feval = 00806
iter = 0403, obj = 4.05532e-13, rnorm = 9.01e-07, gnorm = 2.05e-02, feval = 00808
iter = 0404, obj = 3.81808e-13, rnorm = 8.74e-07, gnorm = 1.10e-02, feval = 00810
iter = 0405, obj = 3.75166e-13, rnorm = 8.66e-07, gnorm = 8.34e-03, feval = 00812
iter = 0406, obj = 3.71874e-13, rnorm = 8.62e-07, gnorm = 3.05e-03, feval = 00814
iter = 0407, obj = 3.71122e-13, rnorm = 8.62e-07, gnorm = 4.02e-03, feval = 00816
iter = 0408, obj = 3.69605e-13, rnorm = 8.60e-07, gnorm = 3.26e-03, feval = 00818
iter = 0409, obj = 3.68958e-13, rnorm = 8.59e-07, gnorm = 3.02e-03, feval = 00820
iter = 0410, obj = 3.68370e-13, rnorm = 8.58e-07, gnorm = 1.79e-03, feval = 00822
iter = 0411, obj = 3.67552e-13, rnorm = 8.57e-07, gnorm = 5.07e-03, feval = 00824
iter = 0412, obj = 3.62704e-13, rnorm = 8.52e-07, gnorm = 8.26e-03, feval = 00826
iter = 0413, obj = 3.53361e-13, rnorm = 8.41e-07, gnorm = 1.31e-02, feval = 00828
iter = 0414, obj = 3.35062e-13, rnorm = 8.19e-07, gnorm = 8.69e-03, feval = 00830
iter = 0415, obj = 3.29676e-13, rnorm = 8.12e-07, gnorm = 1.17e-02, feval = 00832
iter = 0416, obj = 3.07496e-13, rnorm = 7.84e-07, gnorm = 1.22e-02, feval = 00834
iter = 0417, obj = 2.79825e-13, rnorm = 7.48e-07, gnorm = 1.25e-02, feval = 00836
iter = 0418, obj = 2.73747e-13, rnorm = 7.40e-07, gnorm = 6.29e-03, feval = 00838
iter = 0419, obj = 2.68533e-13, rnorm = 7.33e-07, gnorm = 1.25e-02, feval = 00840
iter = 0420, obj = 2.30644e-13, rnorm = 6.79e-07, gnorm = 2.49e-02, feval = 00842
iter = 0421, obj = 1.78410e-13, rnorm = 5.97e-07, gnorm = 3.14e-02, feval = 00844
iter = 0422, obj = 6.67242e-14, rnorm = 3.65e-07, gnorm = 2.46e-02, feval = 00846
iter = 0423, obj = 4.36609e-14, rnorm = 2.96e-07, gnorm = 5.63e-03, feval = 00848
iter = 0424, obj = 4.04943e-14, rnorm = 2.85e-07, gnorm = 6.23e-03, feval = 00850
iter = 0425, obj = 3.68576e-14, rnorm = 2.72e-07, gnorm = 7.50e-03, feval = 00852
iter = 0426, obj = 3.30861e-14, rnorm = 2.57e-07, gnorm = 3.44e-03, feval = 00854
iter = 0427, obj = 3.25568e-14, rnorm = 2.55e-07, gnorm = 2.22e-03, feval = 00856
iter = 0428, obj = 3.22894e-14, rnorm = 2.54e-07, gnorm = 7.05e-04, feval = 00858
iter = 0429, obj = 3.22656e-14, rnorm = 2.54e-07, gnorm = 5.70e-04, feval = 00860
iter = 0430, obj = 3.21875e-14, rnorm = 2.54e-07, gnorm = 8.79e-04, feval = 00862
iter = 0431, obj = 3.19757e-14, rnorm = 2.53e-07, gnorm = 2.64e-03, feval = 00864
iter = 0432, obj = 2.70359e-14, rnorm = 2.33e-07, gnorm = 6.31e-03, feval = 00866
iter = 0433, obj = 2.53153e-14, rnorm = 2.25e-07, gnorm = 3.08e-03, feval = 00868
iter = 0434, obj = 2.50119e-14, rnorm = 2.24e-07, gnorm = 1.63e-03, feval = 00870
iter = 0435, obj = 2.45260e-14, rnorm = 2.21e-07, gnorm = 1.57e-03, feval = 00872
iter = 0436, obj = 2.39502e-14, rnorm = 2.19e-07, gnorm = 3.77e-03, feval = 00874
iter = 0437, obj = 1.99398e-14, rnorm = 2.00e-07, gnorm = 8.07e-03, feval = 00876
iter = 0438, obj = 1.64989e-14, rnorm = 1.82e-07, gnorm = 3.45e-03, feval = 00878
iter = 0439, obj = 1.50793e-14, rnorm = 1.74e-07, gnorm = 5.99e-03, feval = 00880
iter = 0440, obj = 1.19652e-14, rnorm = 1.55e-07, gnorm = 6.92e-03, feval = 00882
iter = 0441, obj = 7.75628e-15, rnorm = 1.25e-07, gnorm = 5.79e-03, feval = 00884
iter = 0442, obj = 3.26849e-15, rnorm = 8.09e-08, gnorm = 4.98e-03, feval = 00886
iter = 0443, obj = 1.96500e-15, rnorm = 6.27e-08, gnorm = 1.15e-03, feval = 00888
iter = 0444, obj = 1.89977e-15, rnorm = 6.16e-08, gnorm = 7.11e-04, feval = 00890
iter = 0445, obj = 1.79183e-15, rnorm = 5.99e-08, gnorm = 1.01e-03, feval = 00892
iter = 0446, obj = 1.73697e-15, rnorm = 5.89e-08, gnorm = 1.02e-03, feval = 00894
iter = 0447, obj = 1.49079e-15, rnorm = 5.46e-08, gnorm = 2.57e-03, feval = 00896
iter = 0448, obj = 9.77349e-16, rnorm = 4.42e-08, gnorm = 1.03e-03, feval = 00898
iter = 0449, obj = 9.26887e-16, rnorm = 4.31e-08, gnorm = 4.94e-04, feval = 00900
iter = 0450, obj = 8.28870e-16, rnorm = 4.07e-08, gnorm = 1.03e-03, feval = 00902
iter = 0451, obj = 7.57633e-16, rnorm = 3.89e-08, gnorm = 5.36e-04, feval = 00904
iter = 0452, obj = 7.47690e-16, rnorm = 3.87e-08, gnorm = 3.51e-04, feval = 00906
iter = 0453, obj = 7.36963e-16, rnorm = 3.84e-08, gnorm = 2.05e-04, feval = 00908
iter = 0454, obj = 7.35612e-16, rnorm = 3.84e-08, gnorm = 5.11e-05, feval = 00910
iter = 0455, obj = 7.35140e-16, rnorm = 3.83e-08, gnorm = 1.11e-04, feval = 00912
iter = 0456, obj = 7.33973e-16, rnorm = 3.83e-08, gnorm = 1.09e-04, feval = 00914
iter = 0457, obj = 7.33336e-16, rnorm = 3.83e-08, gnorm = 8.36e-05, feval = 00916
iter = 0458, obj = 7.31843e-16, rnorm = 3.83e-08, gnorm = 9.49e-05, feval = 00918
iter = 0459, obj = 7.31347e-16, rnorm = 3.82e-08, gnorm = 9.11e-05, feval = 00920
iter = 0460, obj = 7.30758e-16, rnorm = 3.82e-08, gnorm = 9.93e-05, feval = 00922
iter = 0461, obj = 6.92405e-16, rnorm = 3.72e-08, gnorm = 8.06e-04, feval = 00924
iter = 0462, obj = 6.30754e-16, rnorm = 3.55e-08, gnorm = 1.16e-03, feval = 00926
iter = 0463, obj = 5.39675e-16, rnorm = 3.29e-08, gnorm = 8.36e-04, feval = 00928
iter = 0464, obj = 3.61770e-16, rnorm = 2.69e-08, gnorm = 9.75e-04, feval = 00930
iter = 0465, obj = 3.15836e-16, rnorm = 2.51e-08, gnorm = 6.46e-04, feval = 00932
iter = 0466, obj = 3.01237e-16, rnorm = 2.45e-08, gnorm = 2.42e-04, feval = 00934
iter = 0467, obj = 2.92042e-16, rnorm = 2.42e-08, gnorm = 3.44e-04, feval = 00936
iter = 0468, obj = 2.79823e-16, rnorm = 2.37e-08, gnorm = 5.05e-04, feval = 00938
iter = 0469, obj = 2.62312e-16, rnorm = 2.29e-08, gnorm = 3.25e-04, feval = 00940
iter = 0470, obj = 2.20013e-16, rnorm = 2.10e-08, gnorm = 6.94e-04, feval = 00942
iter = 0471, obj = 2.04881e-16, rnorm = 2.02e-08, gnorm = 2.31e-04, feval = 00944
iter = 0472, obj = 1.89051e-16, rnorm = 1.94e-08, gnorm = 7.43e-04, feval = 00946
iter = 0473, obj = 1.18701e-16, rnorm = 1.54e-08, gnorm = 6.95e-04, feval = 00948
iter = 0474, obj = 8.39335e-17, rnorm = 1.30e-08, gnorm = 5.76e-04, feval = 00950
iter = 0475, obj = 4.70420e-17, rnorm = 9.70e-09, gnorm = 8.63e-04, feval = 00952
iter = 0476, obj = 8.26902e-18, rnorm = 4.07e-09, gnorm = 1.39e-04, feval = 00954
iter = 0477, obj = 7.59483e-18, rnorm = 3.90e-09, gnorm = 9.05e-05, feval = 00956
iter = 0478, obj = 6.94317e-18, rnorm = 3.73e-09, gnorm = 5.33e-05, feval = 00958
iter = 0479, obj = 6.62564e-18, rnorm = 3.64e-09, gnorm = 6.22e-05, feval = 00960
iter = 0480, obj = 6.45186e-18, rnorm = 3.59e-09, gnorm = 3.86e-05, feval = 00962
iter = 0481, obj = 6.19638e-18, rnorm = 3.52e-09, gnorm = 8.14e-05, feval = 00964
iter = 0482, obj = 5.11900e-18, rnorm = 3.20e-09, gnorm = 1.24e-04, feval = 00966
iter = 0483, obj = 3.21854e-18, rnorm = 2.54e-09, gnorm = 1.02e-04, feval = 00968
iter = 0484, obj = 2.89830e-18, rnorm = 2.41e-09, gnorm = 2.92e-05, feval = 00970

iter = 0485, obj = 2.74799e-18, rnorm = 2.34e-09, gnorm = 6.39e-05, feval = 00972
iter = 0486, obj = 2.24175e-18, rnorm = 2.12e-09, gnorm = 6.87e-05, feval = 00974
iter = 0487, obj = 1.78427e-18, rnorm = 1.89e-09, gnorm = 4.58e-05, feval = 00976
iter = 0488, obj = 1.72935e-18, rnorm = 1.86e-09, gnorm = 5.82e-06, feval = 00978
iter = 0489, obj = 1.72792e-18, rnorm = 1.86e-09, gnorm = 3.80e-06, feval = 00980
iter = 0490, obj = 1.72159e-18, rnorm = 1.86e-09, gnorm = 6.84e-06, feval = 00982
iter = 0491, obj = 1.71999e-18, rnorm = 1.85e-09, gnorm = 4.21e-06, feval = 00984
iter = 0492, obj = 1.71820e-18, rnorm = 1.85e-09, gnorm = 3.66e-06, feval = 00986
iter = 0493, obj = 1.71538e-18, rnorm = 1.85e-09, gnorm = 3.85e-06, feval = 00988
iter = 0494, obj = 1.71488e-18, rnorm = 1.85e-09, gnorm = 1.47e-06, feval = 00990
iter = 0495, obj = 1.71463e-18, rnorm = 1.85e-09, gnorm = 1.97e-06, feval = 00992
iter = 0496, obj = 1.71423e-18, rnorm = 1.85e-09, gnorm = 2.39e-06, feval = 00994
iter = 0497, obj = 1.70901e-18, rnorm = 1.85e-09, gnorm = 1.18e-05, feval = 00996
iter = 0498, obj = 1.68729e-18, rnorm = 1.84e-09, gnorm = 1.79e-05, feval = 00998
iter = 0499, obj = 1.66690e-18, rnorm = 1.83e-09, gnorm = 1.72e-05, feval = 01000
iter = 0500, obj = 1.64116e-18, rnorm = 1.81e-09, gnorm = 1.22e-05, feval = 01002
iter = 0501, obj = 1.63390e-18, rnorm = 1.81e-09, gnorm = 1.26e-05, feval = 01004
iter = 0502, obj = 1.59055e-18, rnorm = 1.78e-09, gnorm = 1.86e-05, feval = 01006
iter = 0503, obj = 1.57066e-18, rnorm = 1.77e-09, gnorm = 1.47e-05, feval = 01008
iter = 0504, obj = 1.53570e-18, rnorm = 1.75e-09, gnorm = 1.75e-05, feval = 01010
iter = 0505, obj = 1.48959e-18, rnorm = 1.73e-09, gnorm = 3.45e-05, feval = 01012
iter = 0506, obj = 1.31383e-18, rnorm = 1.62e-09, gnorm = 2.84e-05, feval = 01014
iter = 0507, obj = 1.24966e-18, rnorm = 1.58e-09, gnorm = 2.85e-05, feval = 01016
iter = 0508, obj = 1.22404e-18, rnorm = 1.56e-09, gnorm = 7.72e-06, feval = 01018
iter = 0509, obj = 1.21043e-18, rnorm = 1.56e-09, gnorm = 1.32e-05, feval = 01020
iter = 0510, obj = 1.18727e-18, rnorm = 1.54e-09, gnorm = 1.21e-05, feval = 01022
iter = 0511, obj = 1.17578e-18, rnorm = 1.53e-09, gnorm = 1.38e-05, feval = 01024
iter = 0512, obj = 1.14499e-18, rnorm = 1.51e-09, gnorm = 2.37e-05, feval = 01026
iter = 0513, obj = 9.85113e-19, rnorm = 1.40e-09, gnorm = 4.52e-05, feval = 01028
iter = 0514, obj = 6.99893e-19, rnorm = 1.18e-09, gnorm = 7.27e-05, feval = 01030
iter = 0515, obj = 3.23181e-19, rnorm = 8.04e-10, gnorm = 3.45e-05, feval = 01032
iter = 0516, obj = 2.29682e-19, rnorm = 6.78e-10, gnorm = 4.20e-05, feval = 01034
iter = 0517, obj = 9.35155e-20, rnorm = 4.32e-10, gnorm = 4.19e-05, feval = 01036
iter = 0518, obj = 1.71754e-20, rnorm = 1.85e-10, gnorm = 8.93e-06, feval = 01038
iter = 0519, obj = 7.96273e-21, rnorm = 1.26e-10, gnorm = 7.70e-06, feval = 01040
iter = 0520, obj = 3.77812e-21, rnorm = 8.69e-11, gnorm = 4.87e-06, feval = 01042
iter = 0521, obj = 1.33310e-21, rnorm = 5.16e-11, gnorm = 5.07e-06, feval = 01044
iter = 0522, obj = 4.24434e-22, rnorm = 2.91e-11, gnorm = 2.17e-06, feval = 01046
iter = 0523, obj = 2.36707e-22, rnorm = 2.18e-11, gnorm = 8.52e-07, feval = 01048
iter = 0524, obj = 1.91836e-22, rnorm = 1.96e-11, gnorm = 5.65e-07, feval = 01050
iter = 0525, obj = 1.67103e-22, rnorm = 1.83e-11, gnorm = 4.95e-07, feval = 01052
iter = 0526, obj = 1.47280e-22, rnorm = 1.72e-11, gnorm = 5.52e-07, feval = 01054
iter = 0527, obj = 1.24152e-22, rnorm = 1.58e-11, gnorm = 4.04e-07, feval = 01056
iter = 0528, obj = 1.18713e-22, rnorm = 1.54e-11, gnorm = 1.55e-07, feval = 01058
iter = 0529, obj = 9.86537e-23, rnorm = 1.40e-11, gnorm = 6.48e-07, feval = 01060
iter = 0530, obj = 7.97220e-23, rnorm = 1.26e-11, gnorm = 3.21e-07, feval = 01062
iter = 0531, obj = 7.53422e-23, rnorm = 1.23e-11, gnorm = 1.42e-07, feval = 01064
iter = 0532, obj = 7.10839e-23, rnorm = 1.19e-11, gnorm = 1.57e-07, feval = 01066
iter = 0533, obj = 6.90866e-23, rnorm = 1.18e-11, gnorm = 1.75e-07, feval = 01068
iter = 0534, obj = 6.69278e-23, rnorm = 1.16e-11, gnorm = 2.01e-07, feval = 01070
iter = 0535, obj = 6.34731e-23, rnorm = 1.13e-11, gnorm = 9.26e-08, feval = 01072
iter = 0536, obj = 5.61061e-23, rnorm = 1.06e-11, gnorm = 5.28e-07, feval = 01074
iter = 0537, obj = 1.72560e-23, rnorm = 5.87e-12, gnorm = 4.33e-07, feval = 01076
iter = 0538, obj = 1.12986e-23, rnorm = 4.75e-12, gnorm = 1.52e-07, feval = 01078
iter = 0539, obj = 8.88374e-24, rnorm = 4.22e-12, gnorm = 5.97e-08, feval = 01080
iter = 0540, obj = 8.78987e-24, rnorm = 4.19e-12, gnorm = 1.95e-08, feval = 01082
Objective function didn't reduce, will terminate solver:
	obj_new = 8.78987e-24	obj_cur = 8.78987e-24
##########################################################################################
            CG Solver end
##########################################################################################

SLCG.run(Phi2, verbose=True)

##########################################################################################
            Symmetric CG Solver
    Restart folder: /tmp/restart_2022-04-22T01-50-53.913671/
##########################################################################################

iter = 0000, obj = 0.00000e+00, rnorm = 1.41e+01, feval = 00001
iter = 0001, obj = 2.50000e-01, rnorm = 1.41e+02, feval = 00003
iter = 0002, obj = 4.95025e-01, rnorm = 1.39e+02, feval = 00005
iter = 0003, obj = 7.35125e-01, rnorm = 1.38e+02, feval = 00007
iter = 0004, obj = 9.70350e-01, rnorm = 1.36e+02, feval = 00009
iter = 0005, obj = 1.20075e+00, rnorm = 1.35e+02, feval = 00011
iter = 0006, obj = 1.42638e+00, rnorm = 1.34e+02, feval = 00013
iter = 0007, obj = 1.64728e+00, rnorm = 1.32e+02, feval = 00015
iter = 0008, obj = 1.86350e+00, rnorm = 1.31e+02, feval = 00017
iter = 0009, obj = 2.07510e+00, rnorm = 1.29e+02, feval = 00019
iter = 0010, obj = 2.28213e+00, rnorm = 1.28e+02, feval = 00021
iter = 0011, obj = 2.48463e+00, rnorm = 1.27e+02, feval = 00023
iter = 0012, obj = 2.68265e+00, rnorm = 1.25e+02, feval = 00025
iter = 0013, obj = 2.87625e+00, rnorm = 1.24e+02, feval = 00027
iter = 0014, obj = 3.06548e+00, rnorm = 1.22e+02, feval = 00029
iter = 0015, obj = 3.25038e+00, rnorm = 1.21e+02, feval = 00031
iter = 0016, obj = 3.43100e+00, rnorm = 1.19e+02, feval = 00033
iter = 0017, obj = 3.60740e+00, rnorm = 1.18e+02, feval = 00035
iter = 0018, obj = 3.77963e+00, rnorm = 1.17e+02, feval = 00037
iter = 0019, obj = 3.94773e+00, rnorm = 1.15e+02, feval = 00039
iter = 0020, obj = 4.11175e+00, rnorm = 1.14e+02, feval = 00041
iter = 0021, obj = 4.27175e+00, rnorm = 1.12e+02, feval = 00043
iter = 0022, obj = 4.42778e+00, rnorm = 1.11e+02, feval = 00045
iter = 0023, obj = 4.57988e+00, rnorm = 1.10e+02, feval = 00047
iter = 0024, obj = 4.72810e+00, rnorm = 1.08e+02, feval = 00049
iter = 0025, obj = 4.87250e+00, rnorm = 1.07e+02, feval = 00051
iter = 0026, obj = 5.01313e+00, rnorm = 1.05e+02, feval = 00053
iter = 0027, obj = 5.15003e+00, rnorm = 1.04e+02, feval = 00055
iter = 0028, obj = 5.28325e+00, rnorm = 1.03e+02, feval = 00057
iter = 0029, obj = 5.41285e+00, rnorm = 1.01e+02, feval = 00059
iter = 0030, obj = 5.53887e+00, rnorm = 9.97e+01, feval = 00061
iter = 0031, obj = 5.66138e+00, rnorm = 9.83e+01, feval = 00063
iter = 0032, obj = 5.78040e+00, rnorm = 9.69e+01, feval = 00065
iter = 0033, obj = 5.89600e+00, rnorm = 9.55e+01, feval = 00067
iter = 0034, obj = 6.00822e+00, rnorm = 9.40e+01, feval = 00069
iter = 0035, obj = 6.11713e+00, rnorm = 9.26e+01, feval = 00071
iter = 0036, obj = 6.22275e+00, rnorm = 9.12e+01, feval = 00073
iter = 0037, obj = 6.32515e+00, rnorm = 8.98e+01, feval = 00075
iter = 0038, obj = 6.42438e+00, rnorm = 8.84e+01, feval = 00077
iter = 0039, obj = 6.52048e+00, rnorm = 8.70e+01, feval = 00079
iter = 0040, obj = 6.61350e+00, rnorm = 8.56e+01, feval = 00081
iter = 0041, obj = 6.70350e+00, rnorm = 8.41e+01, feval = 00083
iter = 0042, obj = 6.79053e+00, rnorm = 8.27e+01, feval = 00085
iter = 0043, obj = 6.87463e+00, rnorm = 8.13e+01, feval = 00087
iter = 0044, obj = 6.95585e+00, rnorm = 7.99e+01, feval = 00089
iter = 0045, obj = 7.03425e+00, rnorm = 7.85e+01, feval = 00091
iter = 0046, obj = 7.10988e+00, rnorm = 7.71e+01, feval = 00093
iter = 0047, obj = 7.18278e+00, rnorm = 7.57e+01, feval = 00095
iter = 0048, obj = 7.25300e+00, rnorm = 7.42e+01, feval = 00097
iter = 0049, obj = 7.32060e+00, rnorm = 7.28e+01, feval = 00099
iter = 0050, obj = 7.38563e+00, rnorm = 7.14e+01, feval = 00101
iter = 0051, obj = 7.44813e+00, rnorm = 7.00e+01, feval = 00103
iter = 0052, obj = 7.50815e+00, rnorm = 6.86e+01, feval = 00105
iter = 0053, obj = 7.56575e+00, rnorm = 6.72e+01, feval = 00107
iter = 0054, obj = 7.62098e+00, rnorm = 6.58e+01, feval = 00109
iter = 0055, obj = 7.67388e+00, rnorm = 6.43e+01, feval = 00111
iter = 0056, obj = 7.72450e+00, rnorm = 6.29e+01, feval = 00113
iter = 0057, obj = 7.77290e+00, rnorm = 6.15e+01, feval = 00115
iter = 0058, obj = 7.81913e+00, rnorm = 6.01e+01, feval = 00117
iter = 0059, obj = 7.86323e+00, rnorm = 5.87e+01, feval = 00119
iter = 0060, obj = 7.90525e+00, rnorm = 5.73e+01, feval = 00121
iter = 0061, obj = 7.94525e+00, rnorm = 5.59e+01, feval = 00123
iter = 0062, obj = 7.98328e+00, rnorm = 5.44e+01, feval = 00125
iter = 0063, obj = 8.01938e+00, rnorm = 5.30e+01, feval = 00127
iter = 0064, obj = 8.05360e+00, rnorm = 5.16e+01, feval = 00129
iter = 0065, obj = 8.08600e+00, rnorm = 5.02e+01, feval = 00131
iter = 0066, obj = 8.11663e+00, rnorm = 4.88e+01, feval = 00133
iter = 0067, obj = 8.14553e+00, rnorm = 4.74e+01, feval = 00135
iter = 0068, obj = 8.17275e+00, rnorm = 4.60e+01, feval = 00137
iter = 0069, obj = 8.19835e+00, rnorm = 4.45e+01, feval = 00139
iter = 0070, obj = 8.22238e+00, rnorm = 4.31e+01, feval = 00141
iter = 0071, obj = 8.24488e+00, rnorm = 4.17e+01, feval = 00143
iter = 0072, obj = 8.26590e+00, rnorm = 4.03e+01, feval = 00145
iter = 0073, obj = 8.28550e+00, rnorm = 3.89e+01, feval = 00147
iter = 0074, obj = 8.30373e+00, rnorm = 3.75e+01, feval = 00149
iter = 0075, obj = 8.32063e+00, rnorm = 3.61e+01, feval = 00151
iter = 0076, obj = 8.33625e+00, rnorm = 3.46e+01, feval = 00153
iter = 0077, obj = 8.35065e+00, rnorm = 3.32e+01, feval = 00155
iter = 0078, obj = 8.36388e+00, rnorm = 3.18e+01, feval = 00157
iter = 0079, obj = 8.37598e+00, rnorm = 3.04e+01, feval = 00159
iter = 0080, obj = 8.38700e+00, rnorm = 2.90e+01, feval = 00161
iter = 0081, obj = 8.39700e+00, rnorm = 2.76e+01, feval = 00163
iter = 0082, obj = 8.40603e+00, rnorm = 2.62e+01, feval = 00165
iter = 0083, obj = 8.41413e+00, rnorm = 2.47e+01, feval = 00167
iter = 0084, obj = 8.42135e+00, rnorm = 2.33e+01, feval = 00169
iter = 0085, obj = 8.42775e+00, rnorm = 2.19e+01, feval = 00171
iter = 0086, obj = 8.43338e+00, rnorm = 2.05e+01, feval = 00173
iter = 0087, obj = 8.43828e+00, rnorm = 1.91e+01, feval = 00175
iter = 0088, obj = 8.44250e+00, rnorm = 1.77e+01, feval = 00177
iter = 0089, obj = 8.44610e+00, rnorm = 1.62e+01, feval = 00179
iter = 0090, obj = 8.44913e+00, rnorm = 1.48e+01, feval = 00181
iter = 0091, obj = 8.45163e+00, rnorm = 1.34e+01, feval = 00183
iter = 0092, obj = 8.45365e+00, rnorm = 1.20e+01, feval = 00185
iter = 0093, obj = 8.45525e+00, rnorm = 1.06e+01, feval = 00187
iter = 0094, obj = 8.45648e+00, rnorm = 9.17e+00, feval = 00189
iter = 0095, obj = 8.45738e+00, rnorm = 7.75e+00, feval = 00191
iter = 0096, obj = 8.45800e+00, rnorm = 6.32e+00, feval = 00193
iter = 0097, obj = 8.45840e+00, rnorm = 4.90e+00, feval = 00195
iter = 0098, obj = 8.45863e+00, rnorm = 3.46e+00, feval = 00197
iter = 0099, obj = 8.45873e+00, rnorm = 2.00e+00, feval = 00199
iter = 0100, obj = 8.45875e+00, rnorm = 4.71e-16, feval = 00201
Objective function variation not monotonic, will terminate solver:
	obj_old=8.45873e+00	obj_cur=8.45875e+00	obj_new=8.45875e+00
##########################################################################################
            Symmetric CG Solver end
##########################################################################################

fig, ax = plt.subplots()
ax.semilogy((LCGsolver.obj / LCGsolver.obj[0]))
ax.set_xlabel("iteration")
ax.set_xlim(0)
plt.suptitle(r"$\phi_{LCG}$")
plt.show()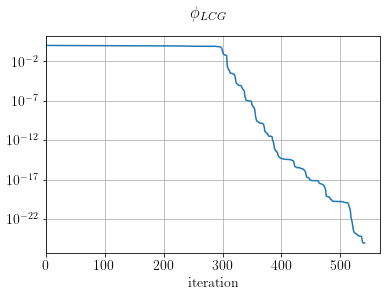

fig, ax = plt.subplots()
ax.plot(SLCG.obj)
ax.set_xlabel("iteration")
ax.set_xlim(0), ax.set_ylim(0,10)
plt.suptitle(r"$\phi_{symLCG}$")
plt.show()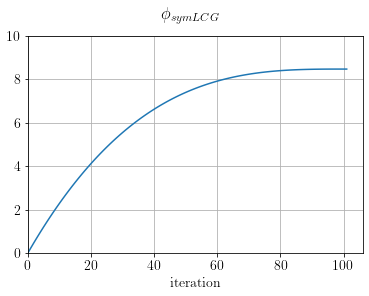

Also, let's compare the two inverted functions with the analytical solution. To find the solution for the continuous case we need three conditions:

\begin{equation} \frac{d^2f(x)}{dx^2}=1,\\ f(x=0)=0,\\ f(x=x_f)=0. \end{equation}

(4)

$x = 0$ and $x = x_f$ are not sampled and lay outside of the interval $\mathbf{x}$ .

X = np.linspace(dx, N*dx, N)
alpha = 0.5
beta  = -(X[-1] + dx) * 0.5
gamma = 0.0
f_an  = alpha * X * X + beta * X + gamma

fig, ax = plt.subplots()

ax.plot(X, Phi1.model.plot(), linewidth=3, label="$\hat{f}(x)$ from $\phi_{LCG}$")
ax.plot(X, Phi2.model.plot(), linewidth=2, dashes=[6, 2], label="$\hat{f}(x)$ from $\phi_{SymLCG}$")
ax.plot(X, f_an, 'k', linewidth=2, dashes=[2, 2], label="Analytical solution")

ax.legend()
ax.set_xlabel(r"$x$"), ax.set_ylabel("$f(x)$")
ax.set_ylim(-0.14, 0), ax.set_xlim(0,1)

plt.suptitle("Inverted functions")
plt.show()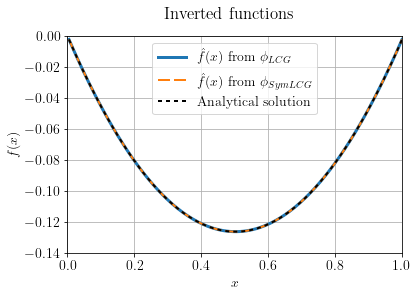

Now, let's try to solve both inversions using the inverse of $D_2$ as a preconditioner

# P = [D_2]^-1
P = o.Matrix(o.VectorNumpy(np.linalg.inv(D2.matrix.getNdArray())), f, y)

Phi1Prec = o.LeastSquares(f.clone(), y, D2, prec=P * P)
Phi2Prec = o.LeastSquaresSymmetric(f.clone(), y, D2, prec=P)

LCGsolver.setDefaults() # Re-setting default solver values
SLCG.setDefaults() # Re-setting default solver values

LCGsolver.run(Phi1Prec, verbose=True)

##########################################################################################
            Preconditioned CG Solver
    Restart folder: /tmp/restart_2022-04-22T01-50-53.913509/
##########################################################################################

iter = 0000, obj = 1.00000e+02, rnorm = 1.41e+01, gnorm = 5.66e+04, feval = 00002
iter = 0001, obj = 1.26970e-22, rnorm = 1.59e-11, gnorm = 2.10e-06, feval = 00004
iter = 0002, obj = 7.95245e-47, rnorm = 1.26e-23, gnorm = 3.61e-19, feval = 00006
Objective function didn't reduce, will terminate solver:
	obj_new = 7.95245e-47	obj_cur = 7.95245e-47
##########################################################################################
            Preconditioned CG Solver end
##########################################################################################

SLCG.run(Phi2Prec, verbose=True)

##########################################################################################
            Preconditioned Symmetric CG Solver
    Restart folder: /tmp/restart_2022-04-22T01-50-53.913671/
##########################################################################################

iter = 0000, obj = 0.00000e+00, rnorm = 1.41e+01, feval = 00001
iter = 0001, obj = 8.45875e+00, rnorm = 1.69e-11, feval = 00003
Objective function variation not monotonic, will terminate solver:
	obj_old=0.00000e+00	obj_cur=8.45875e+00	obj_new=8.45875e+00
##########################################################################################
            Preconditioned Symmetric CG Solver end
##########################################################################################

As expected, we converge to the global minimum in effectively one iteration.

T22 - OccamyPy, an OO optimization framework for large-scale inverse

Notebooks

SplitBregman: enforce sparsity

Simple quadratic problems

Simple quadratic convex problems¶

Instantiation of vectors and operator¶

Importing necessary libraries¶

Inversion tests¶

Instantiation of solver objects¶