# core python 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm, SymLogNorm, Normalize
import ipywidgets

# tools in the simPEG Ecosystem 
import discretize  # for creating computational meshes

# linear solvers
try: 
    from pymatsolver import Pardiso as Solver  # this is a fast linear solver 
except ImportError:
    from SimPEG import SolverLU as Solver  # this will be slower

# SimPEG inversion machinery
from SimPEG import Data, maps

# DC resistivity and IP modules
from SimPEG.electromagnetics import resistivity as dc

# set the font size in the plots
from matplotlib import rcParams
rcParams["font.size"] = 14

line = "46800E"

dc_data_file = f"./century/{line}/{line[:-1]}POT.OBS"

def read_dcip_data(filename, verbose=True):
    """
    Read in a .OBS file from the Century data set into a python dictionary. 
    The format is the old UBC-GIF DCIP format.
    
    Parameters
    ----------
    filename : str
        Path to the file to be parsed
    
    verbose: bool
        Print some things? 
    
    
    Returns
    -------
    dict
        A dictionary with the locations of
        - a_locations: the positive source electrode locations (numpy array) 
        - b_locations: the negative source electrode locations (numpy array) 
        - m_locations: the receiver locations (list of numpy arrays)
        - n_locations: the receiver locations (list of numpy arrays)
        - n_locations: the receiver locations (list of numpy arrays)
        - observed_data: observed data (list of numpy arrays)
        - standard_deviations: assigned standard deviations (list of numpy arrays)
        - n_sources: number of sources (int)
    
    """
    
    # create an empty source_list
    source_list = []
    
    # read in the text file as a numpy array of strings (each row is an entry)
    contents = np.genfromtxt(filename, delimiter=' \n', dtype=np.str)
    
    # the second line has the number of sources, current, and data type (voltages if 1)
    n_sources = int(contents[1].split()[0])
    
    if verbose is True: 
        print(f"number of sources: {n_sources}")
    
    # initialize storage for the electrode locations and data
    a_locations = np.zeros(n_sources)
    b_locations = np.zeros(n_sources)
    m_locations = []
    n_locations = []
    observed_data = []
    standard_deviations = []
    
    # index to track where we have read in content 
    content_index = 1 
    
    # loop over sources 
    for i in range(n_sources):
        # start by reading in the source info 
        content_index = content_index + 1  # read the next line
        a_location, b_location, nrx = contents[content_index].split()  # this is a string

        # convert the strings to a float for locations and an int for the number of receivers
        a_locations[i] = float(a_location)
        b_locations[i] = float(b_location)
        nrx = int(nrx)

        if verbose is True: 
            print(f"Source {i}: A-loc: {a_location}, B-loc: {b_location}, N receivers: {nrx}")

        # initialize space for receiver locations, observed data associated with this source
        m_locations_i, n_locations_i = np.zeros(nrx), np.zeros(nrx)
        observed_data_i, standard_deviations_i = np.zeros(nrx), np.zeros(nrx)

        # read in the receiver info 
        for j in range(nrx):
            content_index = content_index + 1  # read the next line
            m_location, n_location, datum, std = contents[content_index].split()

            # convert the locations and data to floats, and store them
            m_locations_i[j] = float(m_location)
            n_locations_i[j] = float(n_location)
            observed_data_i[j] = float(datum)
            standard_deviations_i[j] = float(std)

        # append the receiver info to the lists
        m_locations.append(m_locations_i)
        n_locations.append(n_locations_i)
        observed_data.append(observed_data_i)
        standard_deviations.append(standard_deviations_i)
    
    return {
        "a_locations": a_locations,
        "b_locations": b_locations, 
        "m_locations": m_locations,
        "n_locations": n_locations,
        "observed_data": observed_data, 
        "standard_deviations": standard_deviations,
        "n_sources": n_sources, 
    }

dc_data_dict = read_dcip_data(dc_data_file, verbose=False)

# initialize an empty list for each 
source_list = []

# center the survey and work in local coordinates
x_local = 0.5*(np.min(dc_data_dict["a_locations"]) + np.max(np.hstack(dc_data_dict["n_locations"])))

for i in range(dc_data_dict["n_sources"]):
    
    # receiver electrode locations in 2D 
    m_locs = np.vstack([
        dc_data_dict["m_locations"][i] - x_local, 
        np.zeros_like(dc_data_dict["m_locations"][i])
    ]).T
    n_locs = np.vstack([
        dc_data_dict["n_locations"][i] - x_local,
        np.zeros_like(dc_data_dict["n_locations"][i])
    ]).T
    
    # construct the receiver object 
    receivers = dc.receivers.Dipole(locations_m=m_locs, locations_n=n_locs, storeProjections=False)
    
    # construct the source 
    source = dc.sources.Dipole(
        location_a=np.r_[dc_data_dict["a_locations"][i] - x_local, 0.],
        location_b=np.r_[dc_data_dict["b_locations"][i] - x_local, 0.],
        receiver_list=[receivers]
    )
    
    # append the new source to the source list
    source_list.append(source)

survey = dc.Survey(source_list=source_list)

def build_mesh(
    survey=survey, 
    n_cells_per_spacing_x=4,
    n_cells_per_spacing_z=4,
    n_core_extra_x=4,
    n_core_extra_z=4,
    core_domain_z_ratio=1/3.,
    padding_factor=1.3,
    n_pad_x=10,
    n_pad_z=10,
):
    """
    A function for designing a Tensor Mesh based on DC survey parameters
    
    Parameters
    ----------
    
    survey: dc.Survey 
        A DC (or IP) survey object
    
    n_cells_per_spacing_[x, z]: int
        Number of [x, z]-cells per the minimum electrode spacing
        
    n_core_extra_[x, z]: int
        Number of extra cells with the same size as the core domain beyond the survey extent
    
    core_domain_z_ratio: float
        Factor that multiplies the maximum AB, MN separation to define the core mesh extent
    
    padding_factor: float
        Factor by which we expand the mesh cells in the padding region
    
    n_pad_[x, z]: int
        Number of padding cells in the x, z directions
    """
    min_electrode_spacing = np.min(np.abs(survey.locations_a[:, 0] - survey.locations_b[:, 0]))

    dx = min_electrode_spacing / n_cells_per_spacing_x
    dz = min_electrode_spacing / n_cells_per_spacing_z
    
    # define the x core domain
    core_domain_x = np.r_[
        survey.electrode_locations[:, 0].min(),
        survey.electrode_locations[:, 0].max()
    ]
    
    # find the y core domain
    # find the maximum spacing between source, receiver midpoints
    mid_ab = (survey.locations_a + survey.locations_b)/2
    mid_mn = (survey.locations_m + survey.locations_n)/2
    separation_ab_mn = np.abs(mid_ab - mid_mn)
    max_separation = separation_ab_mn.max()
    core_domain_z = np.r_[-core_domain_z_ratio * max_separation, 0.]
    
    # add extra cells beyond the core domain
    n_core_x = np.ceil(np.diff(core_domain_x)/dx) + n_core_extra_x*2  # on each side
    n_core_z = np.ceil(np.diff(core_domain_z)/dz) + n_core_extra_z  # just below
    
    # define the tensors in each dimension
    hx = [(dx, n_pad_x, -padding_factor), (dx, n_core_x), (dx, n_pad_x, padding_factor)]
    hz = [(dz, n_pad_z, -padding_factor), (dz, n_core_z)]

    mesh = discretize.TensorMesh([hx, hz], x0="CN")

    return mesh, core_domain_x, core_domain_z

mesh, core_domain_x, core_domain_z = build_mesh(survey)
mesh.plotGrid()

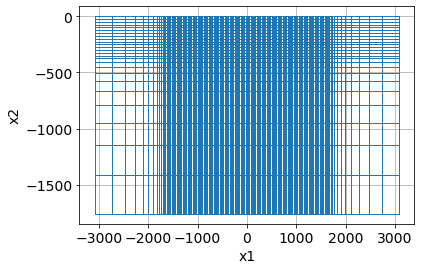
mesh

def forward_simulation_halfspace(mesh, survey=survey, resistivity=100, nky=11):
    """
    A function that  returns predicted data given a mesh, survey, 
    resistivity value and number of filters for the 2.5 DC simulation. 
    """
    # clear the stored source values if they were previously computed 
    for src in survey.source_list:
        src._q = None
        
    rho = resistivity * np.ones(mesh.nC)
    simulation_dc = dc.Simulation2DNodal(
        mesh, rhoMap=maps.IdentityMap(mesh), solver=Solver, 
        survey=survey, nky=nky
    )
    dpred = simulation_dc.make_synthetic_data(rho)
    
    # clear the stored source values if they were previously computed 
    for src in survey.source_list:
        src._q = None
    
    return dpred

def plot_apparent_resistivities(dpred, halfspace_resistivity):
    """
    Plot the apparent resistivity given a SimPEG data object 
    and the true halfspace resistivity. 

    """
    
    # plot psuedosection
    fig = plt.figure(constrained_layout=True, figsize=(12, 4))
    gs = fig.add_gridspec(ncols=3, nrows=1)

    ax0 = fig.add_subplot(gs[:2])
    ax1 = fig.add_subplot(gs[2])

    # plot the pseudosection 
    dc.utils.plot_pseudosection(
        dpred, data_type="apparent resistivity", # clim=clim,
        plot_type="pcolor", data_location=True, ax=ax0, 
    )
    ax0.set_aspect(2)  # some vertical exxageration
    ax0.set_title(f"{line} Pseudosection")
    ax0.set_xlabel("Northing (m)")
    ax0.set_yticks([])

    # plot the errors in apparent resistivity relative to separation
    mid_ab = (survey.locations_a + survey.locations_b)/2
    mid_mn = (survey.locations_m + survey.locations_n)/2
    separation_ab_mn = np.abs(mid_ab - mid_mn)
    apparent_resistivity = dc.utils.apparent_resistivity(dpred)
    percent_error = (apparent_resistivity - halfspace_resistivity)/halfspace_resistivity*100

    ax1.plot(separation_ab_mn[:, 0], percent_error, '.', alpha=0.4)
    ax1.set_xlabel("AB - MN separation")
    ax1.set_ylabel("percent difference (%)")
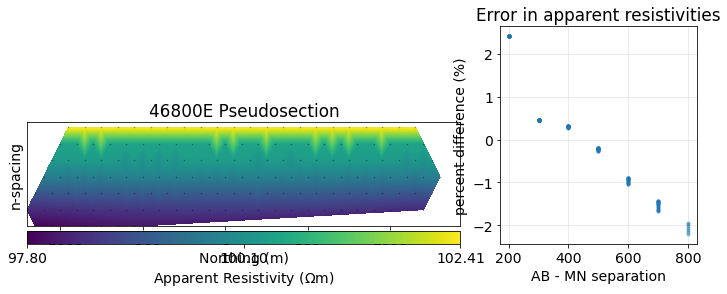
    ax1.set_title("Error in apparent resistivities")
    ax1.grid(alpha=0.3)

halfspace_resistivity = 100
dpred = forward_simulation_halfspace(mesh, resistivity=halfspace_resistivity)
plot_apparent_resistivities(dpred, halfspace_resistivity)

def mesh_design_simulator(
    survey=survey, 
    n_cells_per_spacing_x=4,
    n_cells_per_spacing_z=4,
    n_core_extra_x=4,
    n_core_extra_z=4,
    core_domain_z_ratio=1/3.,
    padding_factor=1.3,
    n_pad_x=10,
    n_pad_z=10,
    log10_halfspace_resistivity=2,
    nky=11,
):
    """
    A function that brings together mesh design and forward simulation so 
    that we can interactively explore factors of mesh design that influence 
    the accuracy of our simulation. 
    """
    
    # set up mesh 
    mesh, core_domain_x, core_domain_z = build_mesh(
        survey=survey, 
        n_cells_per_spacing_x=n_cells_per_spacing_x,
        n_cells_per_spacing_z=n_cells_per_spacing_z,
        n_core_extra_x=n_core_extra_x,
        n_core_extra_z=n_core_extra_z,
        core_domain_z_ratio=core_domain_z_ratio,
        padding_factor=padding_factor,
        n_pad_x=n_pad_x,
        n_pad_z=n_pad_z,
    )
    
    # convert the log10 resistivity to true resistivity on the mesh
    halfspace_resistivity = 10**log10_halfspace_resistivity 
    
    # compute predicted data
    dpred = forward_simulation_halfspace(mesh, resistivity=halfspace_resistivity, nky=nky)
    
    # plot those apparent resistivities 
    plot_apparent_resistivities(dpred, halfspace_resistivity)

mesh_design_app = ipywidgets.interactive(
    mesh_design_simulator,
    survey=ipywidgets.fixed(survey),
    n_cells_per_spacing_x=ipywidgets.IntSlider(
        description="nCx p. 100m", min=1, max=10, value=4, continuous_update=False
    ),
    n_cells_per_spacing_z=ipywidgets.IntSlider(
        description="nCz p. 100m", min=1, max=10, value=4, continuous_update=False
    ),
    n_core_extra_x=ipywidgets.IntSlider(
        description="ncore x +", min=0, max=10, value=4, continuous_update=False
    ),
    n_core_extra_z=ipywidgets.IntSlider(
        description="ncore z +", min=0, max=10, value=4, continuous_update=False
    ),
    core_domain_z_ratio=ipywidgets.FloatSlider(
        description="Dz*maxABMN", min=0.1, max=1, value=0.3, continuous_update=False
    ),
    padding_factor=ipywidgets.FloatSlider(
        description="pad factor", min=1, max=5, value=1.3, continuous_update=False
    ),
    n_pad_x=ipywidgets.IntSlider(
        min=1, max=20, value=10, continuous_update=False
    ),
    n_pad_z=ipywidgets.IntSlider(
        min=1, max=20, value=10, continuous_update=False
    ),
    log10_halfspace_resistivity=ipywidgets.FloatSlider(
        description="$log_{10}\\rho$", min=-1, max=7, value=2, continuous_update=False
    ),
    nky=ipywidgets.IntSlider(
        min=1, max=20, value=11, continuous_update=False
    )
)

mesh_design_app

# define the resistivities
rho_background = 100
rho_resistive_block = 1000
rho_conductive_block = 10

# define the geometry of each block
xlim_resistive_block = np.r_[-500, -250]
zlim_resistive_block = np.r_[-250, -100]

xlim_conductive_block = np.r_[250, 500]
zlim_conductive_block = np.r_[-250, -100]

rho = rho_background * np.ones(mesh.nC)

# resistive block
inds_resistive_block = (
    (mesh.gridCC[:, 0] >= xlim_resistive_block.min()) & (mesh.gridCC[:, 0] <= xlim_resistive_block.max()) &
    (mesh.gridCC[:, 1] >= zlim_resistive_block.min()) & (mesh.gridCC[:, 1] <= zlim_resistive_block.max())
)

rho[inds_resistive_block] = rho_resistive_block

# conductive block
inds_conductive_block = (
    (mesh.gridCC[:, 0] >= xlim_conductive_block.min()) & (mesh.gridCC[:, 0] <= xlim_conductive_block.max()) &
    (mesh.gridCC[:, 1] >= zlim_conductive_block.min()) & (mesh.gridCC[:, 1] <= zlim_conductive_block.max())
)

rho[inds_conductive_block] = rho_conductive_block

fig, ax = plt.subplots(1, 1, figsize=(12, 4))
out = mesh.plotImage(np.log10(rho), ax=ax)
plt.colorbar(out[0], ax=ax, label="log$_{10} \\rho$")
ax.set_xlim(core_domain_x)
ax.set_ylim(core_domain_z + np.r_[-100, 0])
ax.set_aspect(1.5)

mapping = maps.IdentityMap(mesh)

# Generate 2.5D DC problem
simulation_dc = dc.Simulation2DNodal(
    mesh, rhoMap=mapping, solver=Solver, survey=survey
)

%%time 

# run the forward simulation over the half-space 
model_background = rho_background * np.ones(mesh.nC)
fields_background = simulation_dc.fields(model_background)
synthetic_data_background = simulation_dc.make_synthetic_data(model_background, f=fields_background)

%%time 

# run the forward simulation over the full model
fields = simulation_dc.fields(rho)
synthetic_data = simulation_dc.make_synthetic_data(rho, f=fields)

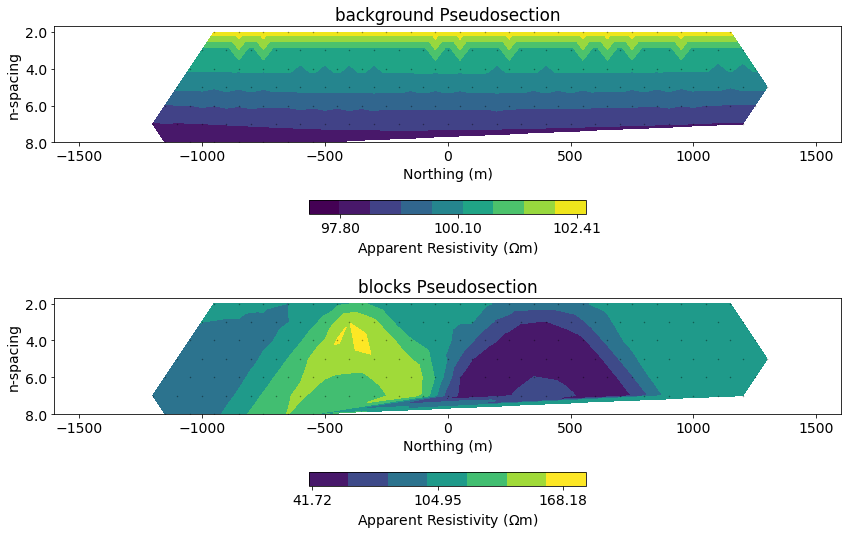
# plot both pseudosections 
fig, ax = plt.subplots(2, 1, figsize=(12, 8))

for a, plot_data, title in zip(
    ax, [synthetic_data_background, synthetic_data], ["background", "blocks"]
):
    
    # plot a psuedosection of the data
    dc.utils.plot_pseudosection(
        plot_data, data_type="apparent resistivity", 
        plot_type="contourf", data_location=True, ax=a, 
        cbar_opts={"pad":0.25}
    )
    a.set_title(f"{title} Pseudosection")
    a.set_xlim(core_domain_x)
    a.set_aspect(1.5)  # some vertical exxageration
    a.set_xlabel("Northing (m)")

plt.tight_layout()

def plot_physics(field="phi", primsec="total", scale="linear", source_ind=0):
    """
    A function for plotting aspects of the forward simulation
    """
    fig, ax = plt.subplots(2, 1, figsize=(12, 8))
    
    pcolor_opts = {}
    view = "real" 
    vType = "CC"
    
    source = survey.source_list[source_ind]
    
    # plotting resistivities
    if field == "model":
        plotme = rho
        if primsec == "primary":
            plotme = model_background
        elif primsec == "secondary":
            plotme = plotme - model_background
        
        if scale.lower() == "log":
            pcolor_opts["norm"] = LogNorm()
            
    # plotting the physics
    else:
        if primsec in ["total", "secondary"]:
            plotme = fields[source, field]
            if primsec == "secondary":
                plotme -= fields_background[source, field]
        else:
            plotme = fields_background[source, field]
                
        # average the potentials to cell centers from Nodes
        if field == "phi": 
            plotme = mesh.aveN2CC * plotme
            
        # average the fields to cell centers
        elif field in ["j", "e"]:
            view = "vec"
            vType = "CCv"
            plotme = mesh.aveE2CCV * plotme
            
            if scale.lower() == "log":
                pcolor_opts["norm"] = LogNorm()
        
        # set an intuitive colorbar for charges
        elif field == "charge_density":
            pcolor_opts["cmap"] = "RdBu_r"
        
        # set a symmetric colorbar
        if field in ["phi", "charge_density"]:
            max_abs = np.abs(plotme).max()
            if scale.lower() == "linear":
                pcolor_opts["norm"] = Normalize(vmin=-max_abs, vmax=max_abs)
            if scale.lower() == "log": 
                pcolor_opts["norm"] = SymLogNorm(
                    linthresh=max_abs * 1e-3, vmin=-max_abs, vmax=max_abs
                )
    
    # plot the physics
    out = mesh.plotImage(
        plotme, view=view, vType=vType, pcolorOpts=pcolor_opts, ax=ax[0], 
        range_x=core_domain_x, range_y=core_domain_z,
    )
    ax[0].plot([source.location_a[0], source.location_b[0]], np.r_[5, 5], "vC3", ms=8)
    ax[0].set_ylim(core_domain_z + np.r_[-100, 0])
    plt.colorbar(out[0], ax=ax[0], label=field, fraction=0.1, orientation="horizontal", pad=0.25)
    
    
    # plot a psuedosection of the data
    dc.utils.plot_pseudosection(
        synthetic_data, data_type="apparent resistivity", # clim=clim,
        plot_type="contourf", data_location=True, ax=ax[1], 
        cbar_opts={"pad":0.25}
    )
    ax[1].set_title(f"{line} Pseudosection")
    
    for a in ax: 
        a.set_xlim(core_domain_x)
        a.set_aspect(1.5)  # some vertical exxageration
        a.set_xlabel("Northing (m)")
    
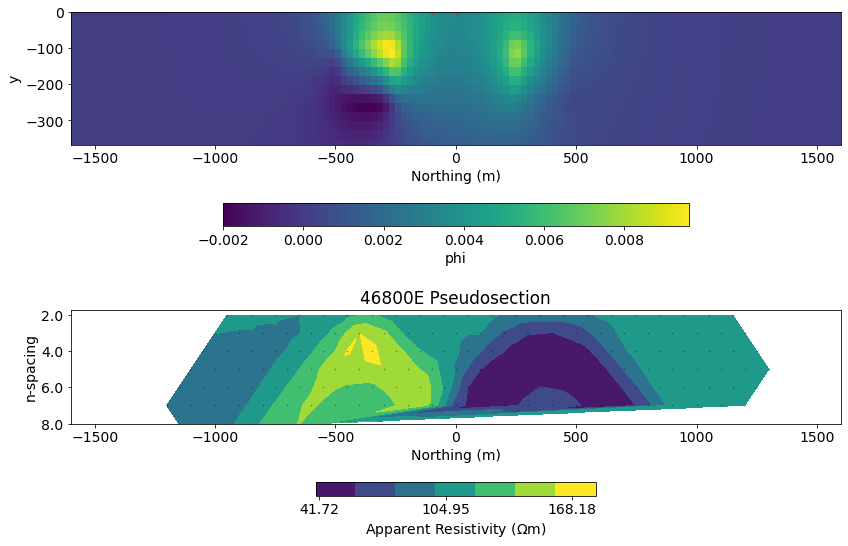
    plt.tight_layout()

plot_physics(field="phi", primsec="secondary", source_ind=15)

dc_physics_app = ipywidgets.interactive(
    plot_physics,
    field=ipywidgets.ToggleButtons(options=["model", "j", "e", "charge_density", "phi"], value="model"),
    primsec=ipywidgets.ToggleButtons(options=["total", "primary", "secondary"], value="total"),
    scale=ipywidgets.ToggleButtons(options=["linear", "log"]),
    source_ind=ipywidgets.IntSlider(min=0, max=len(survey.source_list)-1, value=15),
)

dc_physics_app