Building Operators in PyLops V2: What's New?¶
Author: C. Costa, PyLops Dev Team
The aim of this second tutorial is to introduce you to some features in our latest creation (still in the making): PyLops V2
As any new Major version, there will be breaking changes!
Nevetheless, this is the very first time since the initial creation of PyLops that we decided to sit back and revisit some the early design choices. We hope the benefit introduced by such changes outweights the pain of making a few changes to your codes.
In the following we want to give you a taste of some new features and highlight along the way if (and how) these have required breaking changes.
For more details on how to quickly migrate your PyLops v1.x codes into PyLops v2.x codes please refer to this document.
Useful links¶
Tutorial Github repository: https://github.com/PyLops/pylops_transform2022
PyLops Github repository: https://github.com/PyLops/pylops
PyLops reference documentation: https://pylops.readthedocs.io/en/latest/
Let's Get Shifty¶
To get started, let's suppose we want to implement a simple shift operator. Stating the problem more descriptively, we want an operator that
- Depends on a (possibly fractional) parameter
shift - Can be applied to a vector along a certain given
axis. - A positive
shiftshould shift the vector to the right; a negativeshiftto the left. - The shift is not circular, that is, when shifting to the right, the last samples will not appear in the beginning of the array.
PyLops already features a much fancier Shift operator that works in the Fourier domain, but it is circular.
Numpy offers the roll function, but on its own, it does not support fractional shifts and is also circular.
Note that both of these options could be made non-circular by padding, but for now we're gonna "roll" our own! 😉
Before we jump on creating the operator, let's code a function to do the shift.
After we have the workhorse, it will be easier to write the boilerplate code required for the LinearOperator.
!pip install git+https://github.com/cako/pylops.git@patch-nd-mult numba==0.55.1Collecting git+https://github.com/cako/pylops.git@patch-nd-mult
Cloning https://github.com/cako/pylops.git (to revision patch-nd-mult) to /tmp/pip-req-build-xh0_p0e9
Running command git clone --filter=blob:none -q https://github.com/cako/pylops.git /tmp/pip-req-build-xh0_p0e9
Running command git checkout -b patch-nd-mult --track origin/patch-nd-mult
Switched to a new branch 'patch-nd-mult'
Branch 'patch-nd-mult' set up to track remote branch 'patch-nd-mult' from 'origin'.
Resolved https://github.com/cako/pylops.git to commit 7eda999e99dee796ccf4f71043183aadf97037f1
Preparing metadata (setup.py) ... done
Requirement already satisfied: numba==0.55.1 in /srv/conda/envs/notebook/lib/python3.9/site-packages (0.55.1)
Requirement already satisfied: numpy<1.22,>=1.18 in /srv/conda/envs/notebook/lib/python3.9/site-packages (from numba==0.55.1) (1.21.5)
Requirement already satisfied: setuptools in /srv/conda/envs/notebook/lib/python3.9/site-packages (from numba==0.55.1) (61.2.0)
Requirement already satisfied: llvmlite<0.39,>=0.38.0rc1 in /srv/conda/envs/notebook/lib/python3.9/site-packages (from numba==0.55.1) (0.38.0)
Requirement already satisfied: scipy>=1.4.0 in /srv/conda/envs/notebook/lib/python3.9/site-packages (from pylops==1.13.1.dev405+g7eda999) (1.8.0)
Building wheels for collected packages: pylops
Building wheel for pylops (setup.py) ... done
Created wheel for pylops: filename=pylops-1.13.1.dev405+g7eda999-py3-none-any.whl size=214959 sha256=88625f41ce1bf098aa30254722c0eaca714a31c2d16272a8a56e129742543763
Stored in directory: /tmp/pip-ephem-wheel-cache-zfjn8pdi/wheels/35/30/f6/84ed6553141497e631686feaa225dd3bd262f1396bc22822b7
Successfully built pylops
Installing collected packages: pylops
Attempting uninstall: pylops
Found existing installation: pylops 1.18.0
Uninstalling pylops-1.18.0:
Successfully uninstalled pylops-1.18.0
Successfully installed pylops-1.13.1.dev405+g7eda999
# Uncomment for Google Colab
# !pip install -q --upgrade ipympl
# from google.colab import output
# output.enable_custom_widget_manager()%matplotlib inline
# import cupy as cp # Remove if no GPU
import matplotlib.pyplot as plt
import numba
import numpy as np
import numpy.typing as npt
import pylops
from typing import Tuple
plt.style.use('tableau-colorblind10')
np.random.seed(0)!pip install -q --upgrade watermark
%load_ext watermark
%watermark --iversions -wpylops : 1.13.1.dev405+g7eda999
numba : 0.55.1
numpy : 1.21.5
matplotlib: 3.5.1
Watermark: 2.3.0
We're going to start with an integer-based shifting function, which we will exploit later to convert into a fractional shifter. We want this function to be pretty fast, so we're going to pad the original array and pad it with the correct number of zeros.
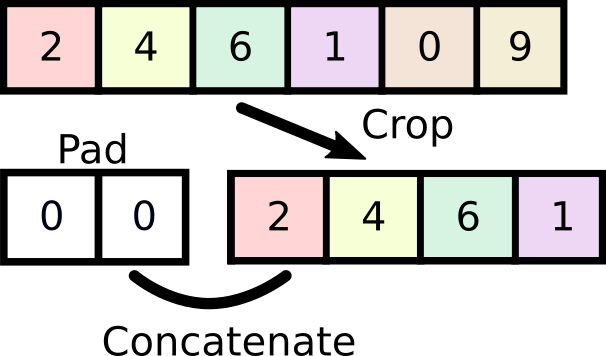
# Original array
x = 1.0 + np.arange(9)
print("Original array:", x)
# Tests for our (integer) shifting method
shift = 3
shifted = np.concatenate((np.zeros(shift), x[:-shift]))
print("Positive shift:", shifted)
shift = -3
shifted = np.concatenate((x[-shift:], np.zeros(-shift)))
print("Negative shift:", shifted)
shift = 0
shifted = np.concatenate((x[-shift:], np.zeros(-shift)))
print("No shift :", shifted)
shift = 12
shifted = np.concatenate((np.zeros(shift), x[:-shift])) # Oops!!
print("Big pos. shift:", shifted)
shift = -12
shifted = np.concatenate((x[-shift:], np.zeros(-shift))) # Oops!!
print("Big neg. shift:", shifted)Original array: [1. 2. 3. 4. 5. 6. 7. 8. 9.]
Positive shift: [0. 0. 0. 1. 2. 3. 4. 5. 6.]
Negative shift: [4. 5. 6. 7. 8. 9. 0. 0. 0.]
No shift : [1. 2. 3. 4. 5. 6. 7. 8. 9.]
Big pos. shift: [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Big neg. shift: [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Now that we know what to do, we can package it into a simple 1D function.
def shift1d(x: npt.NDArray, shift: int):
shift = max(
min(shift, len(x)), -len(x)
) # Fix the oops: ensure shift between -len(x) and len(x)]
if shift > 0:
return np.concatenate((np.zeros(shift), x[:-shift]))
else:
return np.concatenate((x[-shift:], np.zeros(-shift)))
for shift in [3, -3, 0, 12, -12]: # This should be probably be a unit test...
print(shift1d(x, shift))[0. 0. 0. 1. 2. 3. 4. 5. 6.]
[4. 5. 6. 7. 8. 9. 0. 0. 0.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
Looking good! Now we need to make sure this works for N-dimensional arrays. The trick here is to rely on swapaxes (it returns a view, cheap!) and the ellipsis notation. Let's have a go:
x_3d = np.tile(x, (2, 3, 1))
print(x_3d.shape)
x_3d(2, 3, 9)
array([[[1., 2., 3., 4., 5., 6., 7., 8., 9.],
[1., 2., 3., 4., 5., 6., 7., 8., 9.],
[1., 2., 3., 4., 5., 6., 7., 8., 9.]],
[[1., 2., 3., 4., 5., 6., 7., 8., 9.],
[1., 2., 3., 4., 5., 6., 7., 8., 9.],
[1., 2., 3., 4., 5., 6., 7., 8., 9.]]])shift = 4
axis = -1 # Last axis
x_3d_tmp = np.swapaxes(x_3d, axis, -1) # It's view, chill
x_3d_crop = x_3d_tmp[..., :-shift] # Same as x_3d_tmp[:, :, :-shift] for 3D arrays
pad_shape = list(x_3d.shape)
pad_shape[-1] = abs(shift)
pad = np.zeros(pad_shape)
shifted = np.concatenate((pad, x_3d_crop), axis=-1) # Beware, default is axis=0!
shiftedarray([[[0., 0., 0., 0., 1., 2., 3., 4., 5.],
[0., 0., 0., 0., 1., 2., 3., 4., 5.],
[0., 0., 0., 0., 1., 2., 3., 4., 5.]],
[[0., 0., 0., 0., 1., 2., 3., 4., 5.],
[0., 0., 0., 0., 1., 2., 3., 4., 5.],
[0., 0., 0., 0., 1., 2., 3., 4., 5.]]])Packaging it:
def shiftnd(x: npt.NDArray, shift: int, axis: int = -1):
if shift > x.shape[axis] or shift < -x.shape[axis]:
return np.zeros_like(x)
x = np.swapaxes(x, axis, -1) # Relax, original x is unchanged
pad = np.zeros((*x.shape[:-1], abs(shift)))
if shift > 0:
out = np.concatenate((pad, x[..., :-shift]), axis=-1)
else:
out = np.concatenate((x[..., -shift:], pad), axis=-1)
return np.swapaxes(out, axis, -1)
for shift in [1, 0, -2]: # This should be definitely be a unit test...
print(f"Shift = {shift}")
print("Axis = 0 :")
print(shiftnd(x_3d, shift, axis=0))
print("Axis = -1:")
print(shiftnd(x_3d, shift, axis=-1))
print()Shift = 1
Axis = 0 :
[[[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]]]
Axis = -1:
[[[0. 1. 2. 3. 4. 5. 6. 7. 8.]
[0. 1. 2. 3. 4. 5. 6. 7. 8.]
[0. 1. 2. 3. 4. 5. 6. 7. 8.]]
[[0. 1. 2. 3. 4. 5. 6. 7. 8.]
[0. 1. 2. 3. 4. 5. 6. 7. 8.]
[0. 1. 2. 3. 4. 5. 6. 7. 8.]]]
Shift = 0
Axis = 0 :
[[[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]]
[[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]]]
Axis = -1:
[[[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]]
[[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[1. 2. 3. 4. 5. 6. 7. 8. 9.]]]
Shift = -2
Axis = 0 :
[[[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]]
[[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]]]
Axis = -1:
[[[3. 4. 5. 6. 7. 8. 9. 0. 0.]
[3. 4. 5. 6. 7. 8. 9. 0. 0.]
[3. 4. 5. 6. 7. 8. 9. 0. 0.]]
[[3. 4. 5. 6. 7. 8. 9. 0. 0.]
[3. 4. 5. 6. 7. 8. 9. 0. 0.]
[3. 4. 5. 6. 7. 8. 9. 0. 0.]]]
We're almost done. We figured out how to shift by an integer amount in either direction. To shift a fractional amount, we will linearly interpolate the result of shifting by the floor and ceil of the fractional shift! Let represent the fractional shift operator by shift, and let represent the integer shift operator by . Let represent the fractional amount of the shift.
def shiftnd_linear(x: npt.NDArray, shift: float, axis: int = -1):
shift_floor = int(np.floor(shift))
w = shift - shift_floor
return (1 - w) * shiftnd(x, shift_floor, axis) + w * shiftnd(
x, shift_floor + 1, axis
)
print(x)
print(shiftnd_linear(x, 2.1))
print(shiftnd_linear(x, 8))
print(shiftnd_linear(x, 8.9))
print(shiftnd_linear(x, 9))[1. 2. 3. 4. 5. 6. 7. 8. 9.]
[0. 0. 0.9 1.9 2.9 3.9 4.9 5.9 6.9]
[0. 0. 0. 0. 0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0. 0. 0. 0. 0.1]
[0. 0. 0. 0. 0. 0. 0. 0. 0.]
A Simple LinearOperator¶
In this section we will take what we learned about shifting and package that in a LinearOperator class.
What follows is a fairly generic template that can serve as a basis for implementing a wide array of linear operators.
class LinearShift(pylops.LinearOperator):
"""LinearShift shifts an N-dimensional array by a single real value along a given axis.
Since we are responsible coders, this is the entirety of our very long
and detailed documentation for this class. At least we're annotating...
"""
def __init__(
self,
shift: float,
dims: Tuple[int, ...],
axis: int = -1,
dtype: npt.DTypeLike = np.float32,
name: str = "L", # Not required but good practice since v2.0.0
):
# We need to store these variables for computing the shifts
self.shift = shift
self.axis = axis
# Every operator needs a dtype and a shape. Since v2.0.0, we can instead give
# dims (model shape) *and* dimsd (data shape). `self.shape` is automatically
# inferred as (np.prod(dimsd), np.prod(dims)).
# Calling `super()` will also populate `self.clinear` (defaults to True) and
# `self.explicit` (defaults to False). See the latest documentation:
# https://pylops.readthedocs.io/en/latest/api/generated/pylops.LinearOperator.html
super().__init__(dtype=dtype, dims=dims, dimsd=dims, name=name)
def _matvec(self, x: npt.NDArray):
x = x.reshape(self.dims)
y = shiftnd_linear(x, shift=self.shift, axis=self.axis)
y = y.ravel()
return yIn the new version, we use the name of the operator to describe it:
from pylops.utils.describe import describe
LOp = LinearShift(0.5, dims=x_3d.shape)
describe(LOp)# Taking it for a spin
shifted = (LOp @ x_3d.ravel()).reshape(LOp.dimsd)
shiftedarray([[[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5]],
[[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5],
[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5]]])Great! But what if we try the following?
try:
LOp.T @ shifted.ravel()
except AttributeError:
print("Oops!")Oops!
This is because we need to define both the forward and the adjoint. The good news for us is that the adjoint should just be a negative shift.
class LinearShift(pylops.LinearOperator):
"""LinearShift shifts an N-dimensional array by a single real value along a given axis.
Since we are responsible coders, this is the entirety of our very long
and detailed documentation for this class. At least we're annotating...
"""
def __init__(
self,
shift: float,
dims: Tuple[int, ...],
axis: int = -1,
dtype: npt.DTypeLike = np.float32,
name: str = "L", # Not required but good practice since v2.0.0
):
# We need to store these variables for computing the shifts
self.shift = shift
self.axis = axis
# Every operator needs a dtype and a shape. Since v2.0.0, we can instead give
# dims (model shape) *and* dimsd (data shape). `self.shape` is automatically
# calculated as (np.prod(dimsd), np.prod(dims)).
# Calling `super()` will also populate `self.clinear` (defaults to True) and
# `self.explicit` (defaults to False). See the latest documentation:
# https://pylops.readthedocs.io/en/latest/api/generated/pylops.LinearOperator.html
super().__init__(dtype=dtype, dims=dims, dimsd=dims, name=name)
def _matvec(self, x: npt.NDArray):
x = x.reshape(self.dims)
y = shiftnd_linear(x, shift=self.shift, axis=self.axis)
y = y.ravel()
return y
def _rmatvec(self, y: npt.NDArray):
y = y.reshape(self.dimsd)
# negative shift!
x = shiftnd_linear(y, shift=-self.shift, axis=self.axis)
x = x.ravel()
return x
# Taking it for a spin
LOp = LinearShift(0.5, dims=x_3d.shape)
shifted_back = (LOp.T @ shifted.ravel()).reshape(LOp.dimsd)
shifted_backarray([[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]],
[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]]])Are we done now? Nope! We need to ensure that the operations in _matvec and _rmatvec are actually transposes of each other. To do so, we can use the dottest utility function.
from pylops.utils import dottest
dottest(LOp, verb=True, raiseerror=True)Dot test passed, v^H(Opu)=-1.8444506555541245 - u^H(Op^Hv)=-1.844450655554124
TrueSince it passes the dot test, we're done!
Interestingly enough, we see saw that applying the adjoint in succession to the forward is not an inverse
describe(LOp.T @ LOp)shifted_back_adj = (LOp.T @ LOp @ x_3d.ravel()).reshape(x_3d.shape)
np.allclose(shifted_back_adj, x_3d)Falsefig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x_3d[0, 0, :], label=r"$x$")
ax.plot(shifted_back_adj[0, 0, :], "--", label="$L^T L x$")
ax.legend(loc=2)
fig.tight_layout()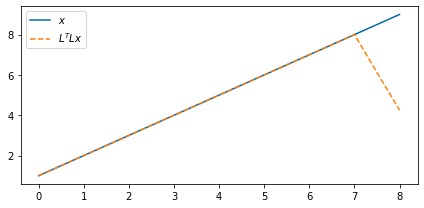
Of course, when we have values at the edges and shift them out of the array we lose them. So in a way, the operator will never have a true inverse. But we can use solvers to aid us in filling this null space. In this case, the least-squares solution we get is the following:
shifted_back_lsqr = (LOp / shifted.ravel()).reshape(LOp.dimsd)fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x_3d[0, 0, :], label=r"$x$")
ax.plot(shifted_back_lsqr[0, 0, :], "--", label="$L^T L x$")
ax.legend(loc=2)
fig.tight_layout()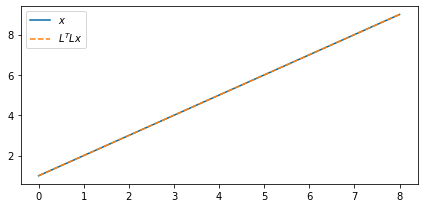
Pretty good, huh?
Ok, but now let's try a harder one.
dims = (20,)
LOp1D = LinearShift(5.9, dims=dims)
x_noise = np.random.uniform(low=1, high=10, size=dims) # Sample away from 0-mean
shifted_noise = LOp1D @ x_noise
shifted_back_noise_adj = LOp1D.T @ shifted_noise
shifted_back_noise_lsqr = LOp1D / shifted_noisefig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x_noise, "k", label=r"$x$")
ax.plot(shifted_back_noise_adj, label=r"$L^T L x$")
ax.plot(shifted_back_noise_lsqr, "--", label="$L$ \ $Lx$")
ax.legend(loc=2)
fig.tight_layout()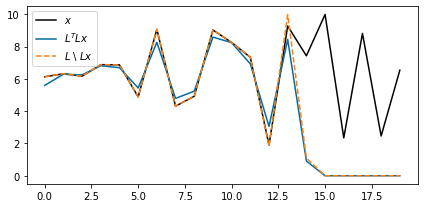
Here we can see that
- Both the least-squares solution () and the adjoint () sets unknown values to be zero (or very close to zero)
- The adjoint solution does not recover the exact values where we did not lose information. This does not happen to the least-squares solution.
The first observation can be explained by the nature of adjoint operator, which pads elements with zero. The least-squares solution does not deviate substantially from this in the null space. Importantly, however, the least-squares solution recovers the signal exactly outside of the null space.
In PyLops, when we call the division operator, we are actually calling an iterative least-squares method — the favored approach when you do not have matrices. There are many other solvers available, some of them showcased in the previous presentation. Find more about them here: https://pylops.readthedocs.io/en/latest/tutorials/solvers.html
For this small operator, we can compute the matrix and use a dense solver to obtain a solution. In large problems, we would not have this choice!
L1D = LOp1D.todense()
shifted_back_noise_dense, *_ = np.linalg.lstsq(L1D, shifted_noise, rcond=None)fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x_noise, "k", label=r"$x$")
ax.plot(shifted_back_noise_adj, label=r"$L^T L x$")
ax.plot(shifted_back_noise_lsqr, "--", label="$L$ \ $Lx$")
ax.plot(shifted_back_noise_dense, "-.", label="$(L^T L)^{-1} x$")
ax.legend(loc=2)
fig.tight_layout()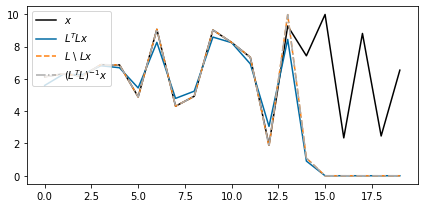
Reshape/Ravel/Reshape/Ravel/...¶
One of the biggest pain points for me when using PyLops often was the reshape/ravel combo that pollutes your code. In PyLops 2.0, we have introduced some changes to alleviate that. Some of these are on the user side:
y = LOp @ x_3d
y.shape(2, 3, 9)In version 1.x, this code would error requiring always x_3d.ravel() as input, and always outputting a flat array. This is what we were doing in this tutorial so far.
The magic 🪄 here is revamped LinearOperator class which understands model dimensions (LOp.dims) and data dimensions (LOp.dimsd). So whereas it still works with flattened arrays, it is now smart enough to reshape internally when needed.
Moreover, it can also "propagate" dims/dimsd across multiple operators, as well as apply to matrices. Here are some examples:
y = LOp.T @ LOp @ x_3d
print(y.shape)
y(2, 3, 9)
array([[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]],
[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]]])X_3d = np.concatenate((x_3d[..., np.newaxis], x_3d[..., np.newaxis]), axis=-1)
X_3d.shape(2, 3, 9, 2)y = LOp.T @ LOp @ X_3d
y.shape(2, 3, 9, 2)The class needs no change, as long as it has a nontrivial dims/dimsd, it will work out of the box. We also included some goodies when implementing new operators. The following pattern is very common:
def _matvec(self, x: npt.NDArray[np.float32]):
x = x.reshape(self.dims)
y = kernel_which_operates_on_reshaped(x)
y = y.ravel()In fact, the following pattern is even more common:
def _matvec(self, x: npt.NDArray[np.float32]):
x = x.reshape(self.dims)
x = x.swapaxes(self.axis, -1)
y = kernel_which_operates_on_reshaped(x)
y.swapaxes(self.axis, -1)
y = y.ravel()The swapaxes is often used so that we can always assume that the axis on which to apply an operation is always the last one.
This creates allows us to use the ellipsis operator in a smart way: we always operate on x[..., i], instead of having to construct indexers.
Previously, we used to do thing like this 🤢:
i_ndim = [ slice(None) ] * len(self.dims)
i_ndim[self.axis] = i
x[i_ndim]Swapaxes is also super cheap since it returns a view of the array.
Using our new reshaped decorator, we can simplify our LinearShift functions from this:
def _matvec(self, x: npt.NDArray[np.float32]):
x = x.reshape(self.dims)
y = shiftnd_linear(x, shift=self.shift, axis=self.axis)
y = y.ravel()
return yto this:
from pylops.utils.decorators import reshaped
⋮
@reshaped
def _matvec(self, x: npt.NDArray[np.float32]):
y = shiftnd_linear(x, shift=self.shift, axis=self.axis)
return yor even this:
from pylops.utils.decorators import reshaped
⋮
@reshaped(swapaxis=True)
def _matvec(self, x: npt.NDArray[np.float32]):
y = shiftnd_linear(x, shift=self.shift, axis=-1)
return yTo finish this tutorial, let's see the full standalone LinearShift operator with some extra goodies.
import logging
import pylops
from math import floor
from pylops.utils.decorators import reshaped
try:
from numba import jit
NUMBA_AVAILABLE = True
except ImportError:
NUMBA_AVAILABLE = False
logger = logging.getLogger()
logger.setLevel(logging.INFO)
class LinearShift(pylops.LinearOperator):
"""LinearShift shifts an N-dimensional array by a single real value along a given axis.
Since we are responsible coders, this is the entirety of our very long
and detailed documentation for this class. At least we're annotating...
"""
def __init__(
self,
shift: float,
dims: Tuple[int, ...],
axis: int = -1,
dtype: npt.DTypeLike = np.float32,
name: str = "L",
engine: str = "numba", # Use numpy for GPU
):
self.shift = shift
self.axis = axis
if engine == "numba" and not NUMBA_AVAILABLE:
engine = "numpy"
logger.warning("Numba engine not available.")
self.engine = engine
logger.info(f"Using {self.engine} engine.")
super().__init__(dtype=dtype, dims=dims, dimsd=dims, name=name)
self._register_shiftnd_linear()
def _register_shiftnd_linear(self):
"""
Register the correct method depending on whether Numba
is available or not.
"""
# CuPy- and Numba-accepted functions: relies only on ndarray properties;
# remove dependency on `np`.
#
# An alternative design choice is to register both a CPU and a GPU method,
# and, inside of _(r)matvec, use cupy.get_array_module(x) to decide which
# method to call.
def shiftnd(x: npt.NDArray, shift: int):
out = x * 0.0 # replaces np.zeros_like
if abs(shift) > x.shape[-1]:
return out
if shift == 0:
out[:] = x[:]
elif shift > 0:
out[..., shift:] = x[..., :-shift]
else:
out[..., :shift] = x[..., -shift:]
return out
def shiftnd_linear(x: npt.NDArray, shift: float):
shift_floor = int(floor(shift))
w = shift - shift_floor
return (1 - w) * shiftnd(x, shift_floor) + w * shiftnd(x, shift_floor + 1)
if self.engine == "numba":
numba_opts = dict(nopython=True, fastmath=True, nogil=True, parallel=True)
shiftnd = jit(**numba_opts)(shiftnd) # Must jit all functions used by `shiftnd_linear`
shiftnd_linear = jit(**numba_opts)(shiftnd_linear)
self._shiftnd_linear = shiftnd_linear
@reshaped(swapaxis=True)
def _matvec(self, x: npt.NDArray):
return self._shiftnd_linear(x, shift=self.shift)
@reshaped(swapaxis=True)
def _rmatvec(self, y: npt.NDArray):
return self._shiftnd_linear(y, shift=-self.shift)# Taking it for a spin: CPU
LOp = LinearShift(0.5, dims=x_3d.shape)
LOp.T @ LOp @ x_3dINFO: Using numba engine.
array([[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]],
[[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25],
[1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 4.25]]])# Taking it for a spin: GPU
LOp = LinearShift(0.5, dims=x_3d.shape, engine="numpy")
x_3d_gpu = cp.asarray(x_3d) # move to GPU
LOp.T @ LOp @ x_3d_gpu
