The Covariance Model

One of the fundamental features of GSTools is the powerful CovModel class, which allows you to easily define arbitrary covariance models by yourself. The resulting models provide a bunch of nice features to explore the covariance models.

A covariance model is used to characterize the semi-variogram, denoted by $\gamma$, of a spatial random field. In GSTools, we use the following formulation for an isotropic and stationary field:

$\gamma\left(r\right)=\sigma^2\cdot\left(1-\mathrm{cor}\left(s\cdot\frac{r}{\ell}\right)\right)+n$

Where:

• $r$ is the lag distance
• $\ell$ is the main correlation length
• $s$ is a scaling factor for unit conversion or normalization
• $\sigma^2$ is the variance
• $n$ is the nugget (subscale variance)
• $\mathrm{cor}(h)$ is the normalized correlation function depending on the non-dimensional distance $h=s\cdot\frac{r}{\ell}$

Depending on the normalized correlation function, all covariance models in GSTools are providing the following functions:

• $\rho(r)=\mathrm{cor}\left(s\cdot\frac{r}{\ell}\right)$ is the so called correlation function
• $C(r)=\sigma^2\cdot\rho(r)$ is the so called covariance function, which gives the name for our GSTools class

.. note::

We are not limited to isotropic models. GSTools supports anisotropy ratios for length scales in orthogonal transversal directions like:

• $x_0$ (main direction)
• $x_1$ (1. transversal direction)
• $x_2$ (2. transversal direction)
• ...

These main directions can also be rotated. Just have a look at the corresponding examples.

Provided Covariance Models¶

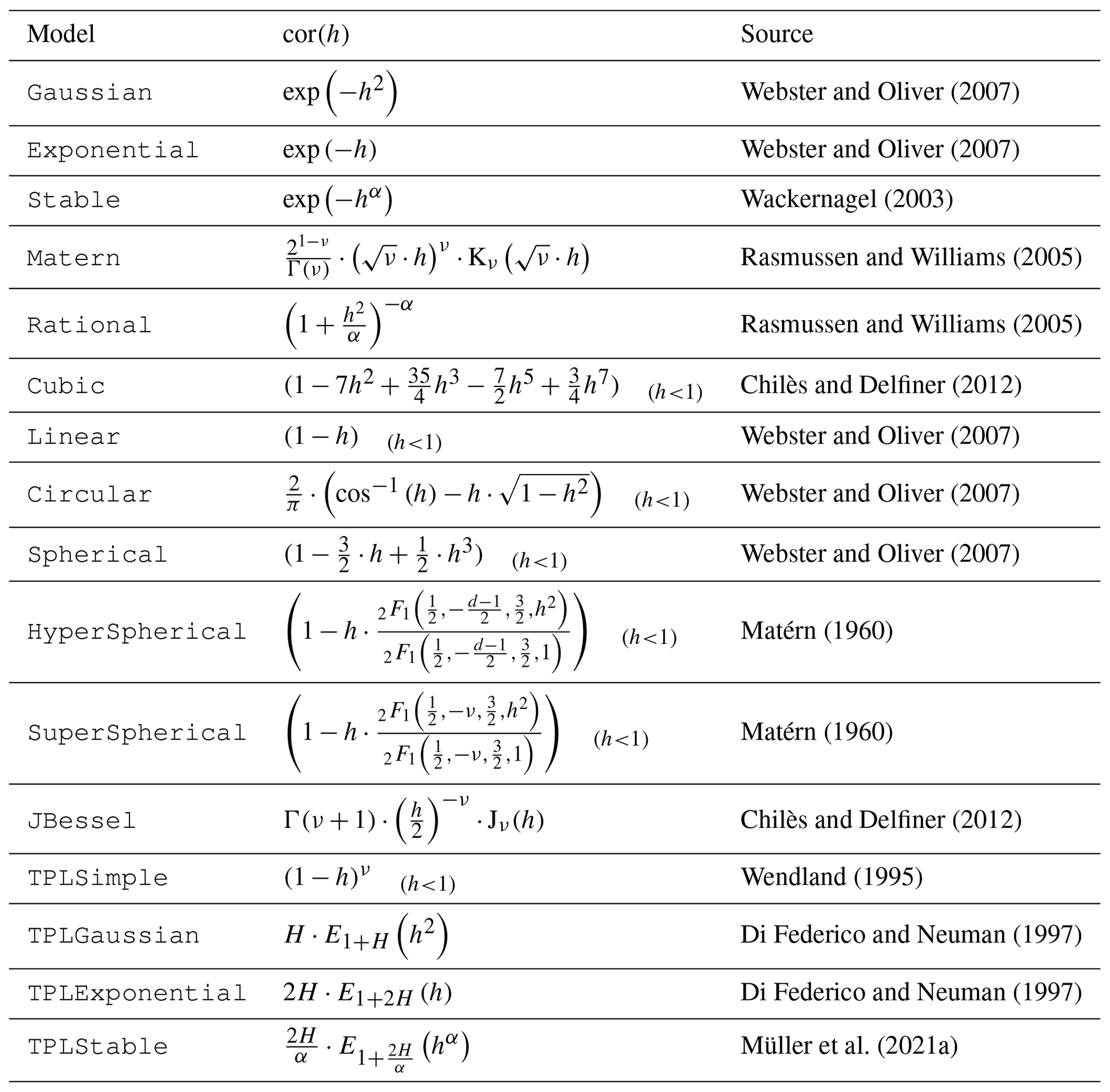
Taken from Müller et al. (2022).