Get in Touch!

Youtube Livestream

Purpose¶

GeoStatTools provides geostatistical tools for various purposes:

• random field generation
• simple, ordinary, universal and external drift kriging
• conditioned field generation
• (automated) variogram estimation and fitting
• data normalization and transformation
• many readily provided and even user-defined covariance models
• metric spatio-temporal modelling
• plotting and exporting routines

Installation¶

We assume, that you already have conda set up and running. Please clone or download this repository to get started.

Installation of conda¶

On Windows, the easiest way to get conda is to install Anaconda with the provided installer from this link. Then open the provided command promt to proceed.

On Unix systems like MacOS or Linux, you can install conda with the following terminal commands:

curl -L -O https://repo.anaconda.com/miniconda/Miniconda3-latest-$(uname)-$(uname -m).sh
bash Miniconda3-latest-$(uname)-$(uname -m).sh  # init conda: yes ; restart shell
conda config --set auto_activate_base false     # otherwise conda is always active

conda environment¶

We provide a conda environment with all needed dependencies for this tutorial. Just create and activate it with:

conda env create --file=environment.yml
conda activate t22-gstools

Then you can start Jupyter-Lab in this environment

jupyter-lab

Citation¶

If you are using GSTools in your publication please cite our paper:

Müller, S., Schüler, L., Zech, A., and Heße, F.:
GSTools v1.3: a toolbox for geostatistical modelling in Python,
Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.

You can cite the Zenodo code publication of GSTools by:

Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628

If you want to cite a specific version, have a look at the Zenodo site.

Documentation for GSTools¶

You can find the documentation under gstools.readthedocs.io.

Intro¶

Spatial Random Field Generation¶

The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by Heße et al. 2014.

Examples¶

Gaussian Covariance Model¶

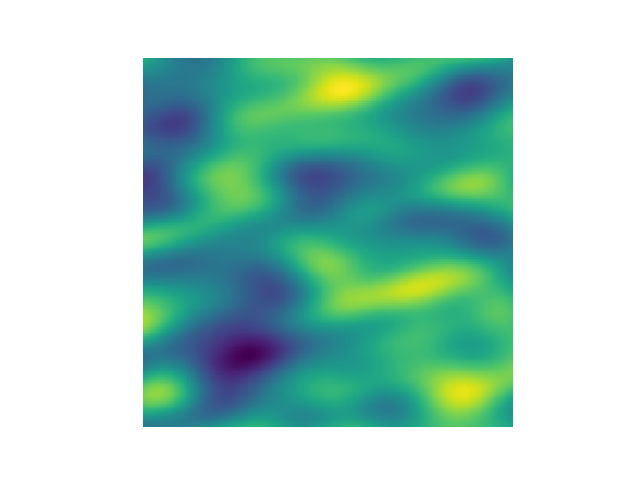
This is an example of how to generate a 2 dimensional spatial random field with a gaussian covariance model.

import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()

GSTools also provides support for geographic coordinates. This works perfectly well with cartopy.

import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import gstools as gs
# define a structured field by latitude and longitude
lat = lon = range(-80, 81)
model = gs.Gaussian(latlon=True, len_scale=777, rescale=gs.EARTH_RADIUS)
srf = gs.SRF(model, seed=12345)
field = srf.structured((lat, lon))
# Orthographic plotting with cartopy
ax = plt.subplot(projection=ccrs.Orthographic(-45, 45))
cont = ax.contourf(lon, lat, field, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_global()
plt.colorbar(cont)

A similar example but for a three dimensional field is exported to a VTK file, which can be visualized with ParaView or PyVista in Python:

import gstools as gs
# structured field with a size 100x100x100 and a grid-size of 1x1x1
x = y = z = range(100)
model = gs.Gaussian(dim=3, len_scale=[16, 8, 4], angles=(0.8, 0.4, 0.2))
srf = gs.SRF(model)
srf((x, y, z), mesh_type='structured')
srf.vtk_export('3d_field') # Save to a VTK file for ParaView

mesh = srf.to_pyvista() # Create a PyVista mesh for plotting in Python
mesh.contour(isosurfaces=8).plot()

Estimating and Fitting Variograms¶

The spatial structure of a field can be analyzed with the variogram, which contains the same information as the covariance function.

All covariance models can be used to fit given variogram data by a simple interface.

Example¶

This is an example of how to estimate the variogram of a 2 dimensional unstructured field and estimate the parameters of the covariance model again.

import numpy as np
import gstools as gs
# generate a synthetic field with an exponential model
x = np.random.RandomState(19970221).rand(1000) * 100.
y = np.random.RandomState(20011012).rand(1000) * 100.
model = gs.Exponential(dim=2, var=2, len_scale=8)
srf = gs.SRF(model, mean=0, seed=19970221)
field = srf((x, y))
# estimate the variogram of the field
bin_center, gamma = gs.vario_estimate((x, y), field)
# fit the variogram with a stable model. (no nugget fitted)
fit_model = gs.Stable(dim=2)
fit_model.fit_variogram(bin_center, gamma, nugget=False)
# output
ax = fit_model.plot(x_max=max(bin_center))
ax.scatter(bin_center, gamma)
print(fit_model)

Which gives:

Stable(dim=2, var=1.85, len_scale=7.42, nugget=0.0, anis=[1.0], angles=[0.0], alpha=1.09)

Kriging and Conditioned Random Fields¶

An important part of geostatistics is Kriging and conditioning spatial random fields to measurements. With conditioned random fields, an ensemble of field realizations with their variability depending on the proximity of the measurements can be generated.

Example¶

For better visualization, we will condition a 1d field to a few "measurements", generate 100 realizations and plot them:

import numpy as np
import matplotlib.pyplot as plt
import gstools as gs

# conditions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]

# conditioned spatial random field class
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
# same output positions for all ensemble members
grid_pos = np.linspace(0.0, 15.0, 151)
cond_srf.set_pos(grid_pos)

# seeded ensemble generation
seed = gs.random.MasterRNG(20170519)
for i in range(100):
    field = cond_srf(seed=seed(), store=f"field_{i}")
    plt.plot(grid_pos, field, color="k", alpha=0.1)
plt.scatter(cond_pos, cond_val, color="k")
plt.show()

User Defined Covariance Models¶

One of the core-features of GSTools is the powerful CovModel class, which allows to easy define covariance models by the user.

Example¶

Here we re-implement the Gaussian covariance model by defining just a correlation function, which takes a non-dimensional distance h = r/l:

import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
    def cor(self, h):
        return np.exp(-h**2)

And that's it! With Gau you now have a fully working covariance model, which you could use for field generation or variogram fitting as shown above.

Have a look at the documentation for further information on incorporating optional parameters and optimizations.

VTK/PyVista Export¶

After you have created a field, you may want to save it to file, so we provide a handy VTK export routine using the .vtk_export() or you could create a VTK/PyVista dataset for use in Python with to .to_pyvista() method:

import gstools as gs
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.vtk_export("field") # Saves to a VTK file
mesh = srf.to_pyvista() # Create a VTK/PyVista dataset in memory
mesh.plot()

Which gives a RectilinearGrid VTK file field.vtr or creates a PyVista mesh in memory for immediate 3D plotting in Python.

Contact¶

You can contact us via info@geostat-framework.org.

License¶

LGPLv3 © 2018-2021